Estimate geodetic time series from the Nevada Geodetic Laboratory • gmwmx2

Model and estimator

This vignette builds on the general framework described in the vignettes “Estimate linear models with dependent errors” and “Estimate linear models with dependent errors and missing observations”. We do not repeat the full model, missingness mechanism, or estimation details here. Please refer to these vignettes for the formal setup, and use this one as a hands-on guide for geodetic time series from the Nevada Geodetic Laboratory.

Estimating tectonic velocities and crustal uplift

While the GMWMX, as described above and in more detail in Voirol et al. (2024), is a general method for estimating large linear models with complex dependence structures in presence of missing observations, the gmwmx2 R package allows to estimate tectonic velocities and crustal uplift from position time series in graticule distance (GD) coordinates provided by the Nevada Geodetic Laboratory (Blewitt 2024; Blewitt, Hammond, and Kreemer 2018).

Trajectory model

To estimate the trajectory model (see, e.g., Bevis and Brown (2014) for more details), we construct the design matrix $\boldsymbol{X}$ such that the $i$ -th component of the vector $\mathbf{X} {{\boldsymbol{\beta}}}$ can be described as follows, with $t_i$ representing the $i^{\text{th}}$ ordered time point (epoch) in Modified Julian Date and $t_0$ representing the reference epoch located exactly in the middle of the start and end points of the time series:

\begin{split} \mathbb{E}[\mathbf{Y}_i] &= \mathbf{X}_i^T {{\boldsymbol{\beta}}} \\ &= a + b \left(t_{i} - t_0\right) + \sum_{h=1}^{m}\left[c_{h} \sin \left(2 \pi f_{h} t_{i}\right) + d_h \cos \left(2 \pi f_h t_i\right)\right] + \\& \sum_{j=1}^{r}e_j H\left(t_i - t_j\right) + \sum_{k = 1 }^{s} l_k \left[1- \exp\left(\frac{-(t_i-t_k)}{\tau_k}\right)\right]H\left(t_{i}-\tau_k\right) \end{split}

where $a$ is the initial position at the reference epoch $t_0$ , $b$ is the velocity parameter, and $c_h$ and $d_h$ are the periodic motion parameters ( $h = 1$ and $h = 2$ represent the annual and semi-annual seasonal terms, respectively with $f_1 = \frac{1}{365.25}$ and $f_2 = \frac{2}{365.25}$ ). The offset terms model earthquakes, equipment changes, or human intervention, in which $e_j$ is the magnitude of the step at epochs $t_j$ , $r$ is the total number of offsets, and $H$ is the Heaviside step function defined as $H(x):= \begin{cases}1, & x \geq 0 \\ 0, & x<0\end{cases}$ . The last term allows us to model post-seismic deformation (see, e.g., Sobrero et al. (2020)) where $s$ is the number of post-seismic relaxation times specified, $t_k$ is the time when the relaxation $k$ starts in Modified Julian Date (MJD), $\tau_k$ is the relaxation period in days for the post-seismic relaxation $k$ , and $l_k$ is the amplitude of the transient. Note that by default the estimates of the functional parameters are provided in units/day.

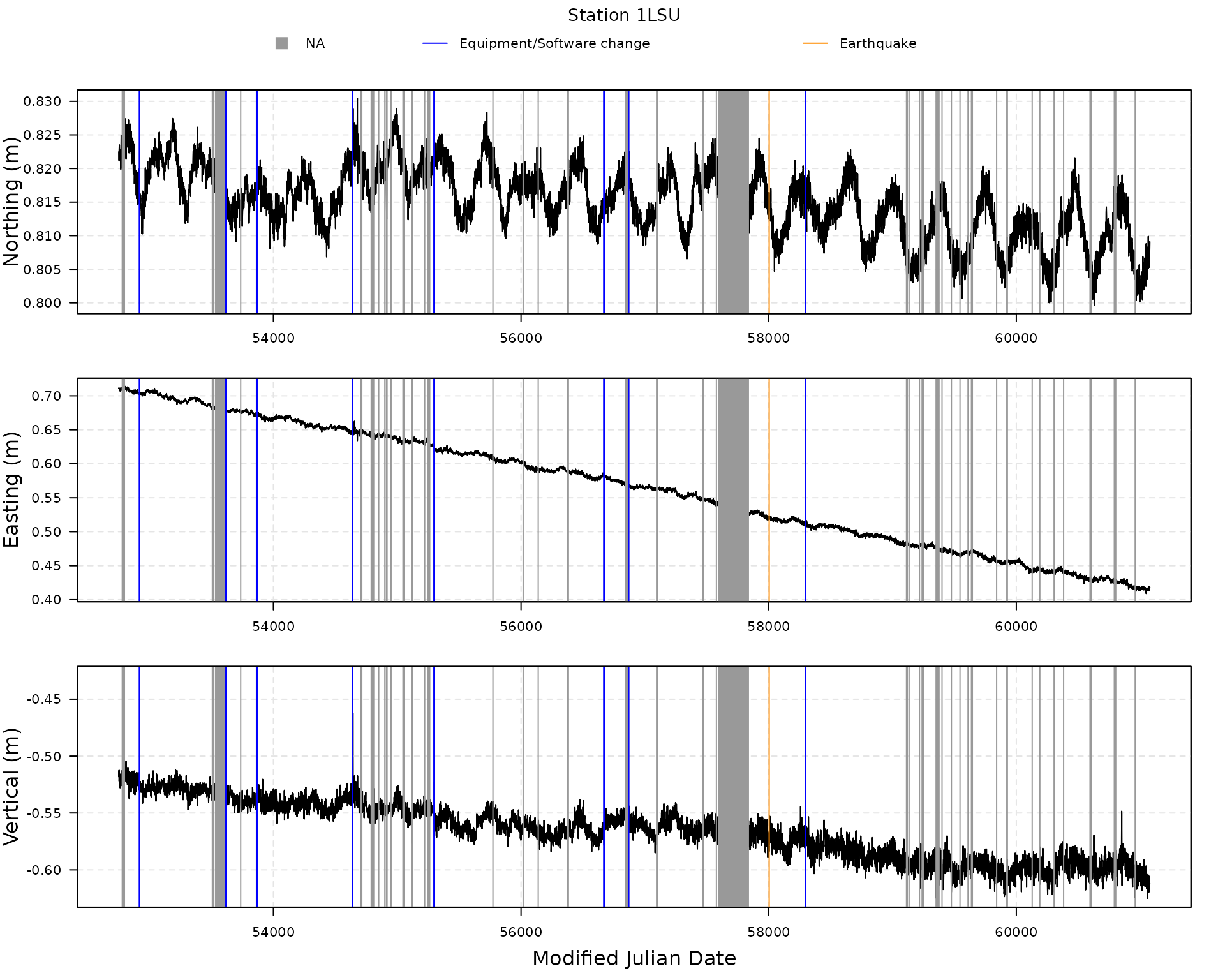
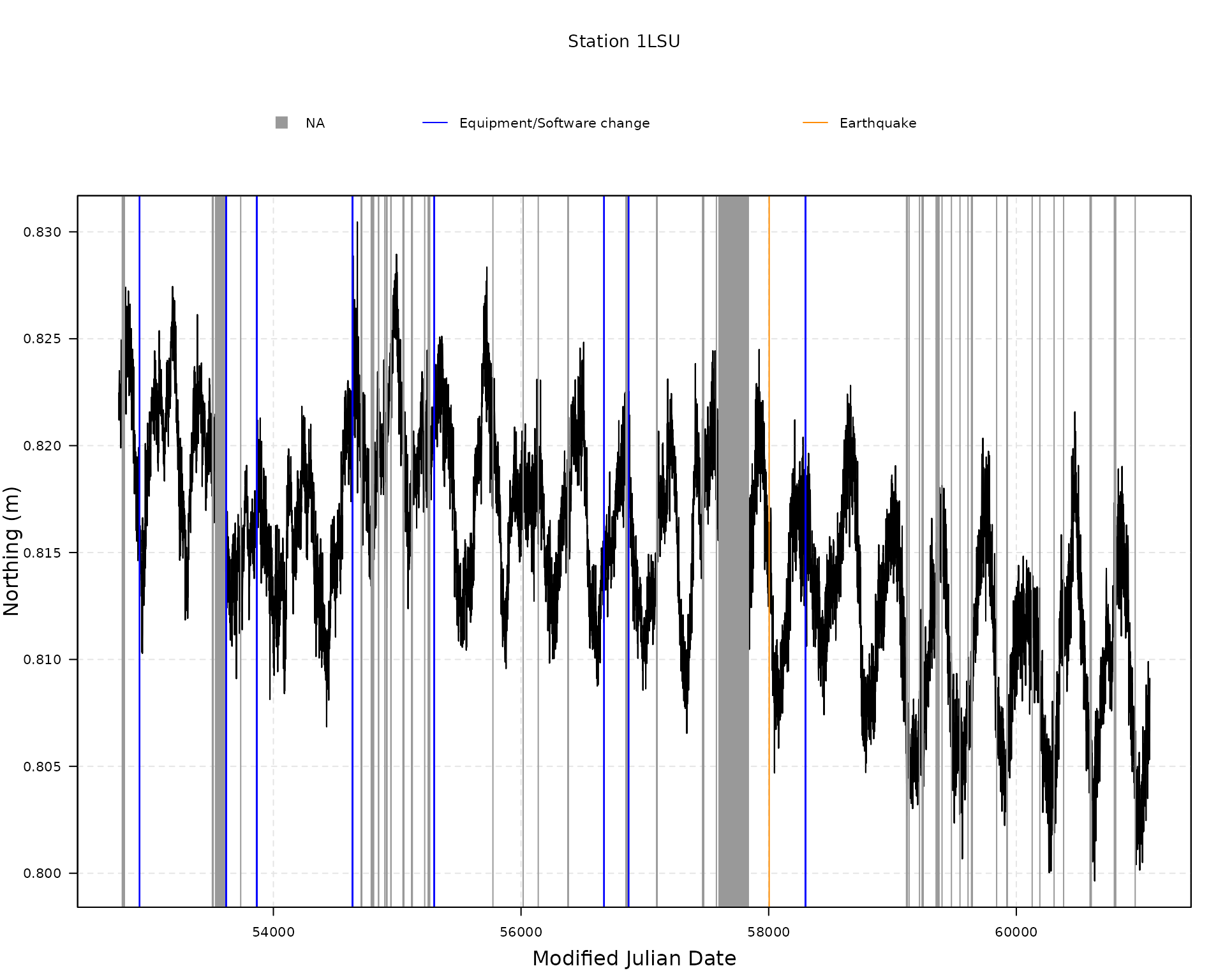
When loading data from a specific station using gmwmx2::download_station_ngl(), we extract from the Nevada Geodetic Laboratory the position time series in GD coordinates, the time steps associated with equipment or software changes, and the time steps associated with earthquakes near the station. All these objects are stored in an object of class gnss_ts_ngl.

When applying the function gmwmx2::gmwmx2() to an object of class gnss_ts_ngl, we construct the design matrix $\boldsymbol{X}$ by considering an offset term for all equipment or software change steps and all earthquakes indicated by the NGL. We also specify a post-seismic relaxation term for all earthquakes indicated by the NGL. If no relaxation time is specified in the argument vec_earthquakes_relaxation_time, we use a default relaxation time of $365.25$ days.

Stochastic model

It is generally recognized that noise in GNSS time series is best described by a combination of colored noise plus white noise (He et al. 2017; Langbein 2008; Williams et al. 2004; Bos et al. 2013), where the white noise generally models noise at high frequencies and the colored noise models the lower frequencies of the spectrum.

In gmwmx2, you can pass any valid stochastic model to the estimator: either a single time-series model (e.g., wn(), ar1(), pl(), matern(), rw(), flicker()) or a composite sum model built with + (e.g., wn() + pl() or wn() + ar1() + rw()). This makes the stochastic specification very general and easy to adapt to your application.

Example of estimation

Let us showcase how to estimate tectonic velocity for one specific component (North, East, or Vertical) of one station.

First, load the gmwmx2 package.

library(gmwmx2)

Download a station from Nevada Geodetic Laboratory

station_data <- download_station_ngl("1LSU")

Plot Station

plot(station_data)

Plot Northing component

plot(station_data, component = "N")

Estimate models on station data

fit1 <- gmwmx2(station_data, n_seasonal = 2, component = "N", model = wn())
fit1

## GMWMX fit GNSS Times Series (Nevada Geodetic Laboratory)
##                         Estimate Std.Error   CI.Lower   CI.Upper
## Intercept              8.156e-01 1.788e-04  8.152e-01  8.159e-01
## Trend                 -1.090e-06 3.588e-08 -1.160e-06 -1.019e-06
## Sin (Annual)          -5.216e-04 2.092e-05 -5.626e-04 -4.806e-04
## Cos (Annual)          -4.129e-03 2.091e-05 -4.170e-03 -4.088e-03
## Sin (Semi-Annual)      1.089e-03 2.057e-05  1.049e-03  1.129e-03
## Cos (Semi-Annual)     -4.455e-04 2.057e-05 -4.858e-04 -4.051e-04
## Jump: MJD 52920        4.958e-04 1.157e-04  2.691e-04  7.226e-04
## Jump: MJD 53619       -3.057e-03 9.985e-05 -3.253e-03 -2.861e-03
## Jump: MJD 53866       -5.586e-04 9.908e-05 -7.528e-04 -3.644e-04
## Jump: MJD 54637       -2.499e-04 7.663e-04 -1.752e-03  1.252e-03
## Jump: MJD 54640        6.393e-03 7.666e-04  4.890e-03  7.895e-03
## Jump: MJD 55300       -2.496e-03 7.267e-05 -2.639e-03 -2.354e-03
## Jump: MJD 56671       -1.193e-03 1.057e-04 -1.400e-03 -9.857e-04
## Jump: MJD 56868        1.120e-03 1.055e-04  9.134e-04  1.327e-03
## Jump: MJD 58298        3.321e-03 1.753e-04  2.977e-03  3.664e-03
## Jump: MJD 58004        1.137e-03 1.162e-04  9.096e-04  1.365e-03
## Earthquake: MJD 58004 -7.135e-03 2.909e-04 -7.705e-03 -6.565e-03
## 
## Missingness model
##   Proportion missing : 0.0584 
##   p1                 : 0.0073 
##   p2                 : 0.1173 
##   p*                 : 0.9416 
## 
## Stochastic model
##   Model      : White Noise 
##   Parameters : sigma2 = 1.65e-06 
## 
## Runtime (seconds)
##   Total              : 2.5790

plot(fit1)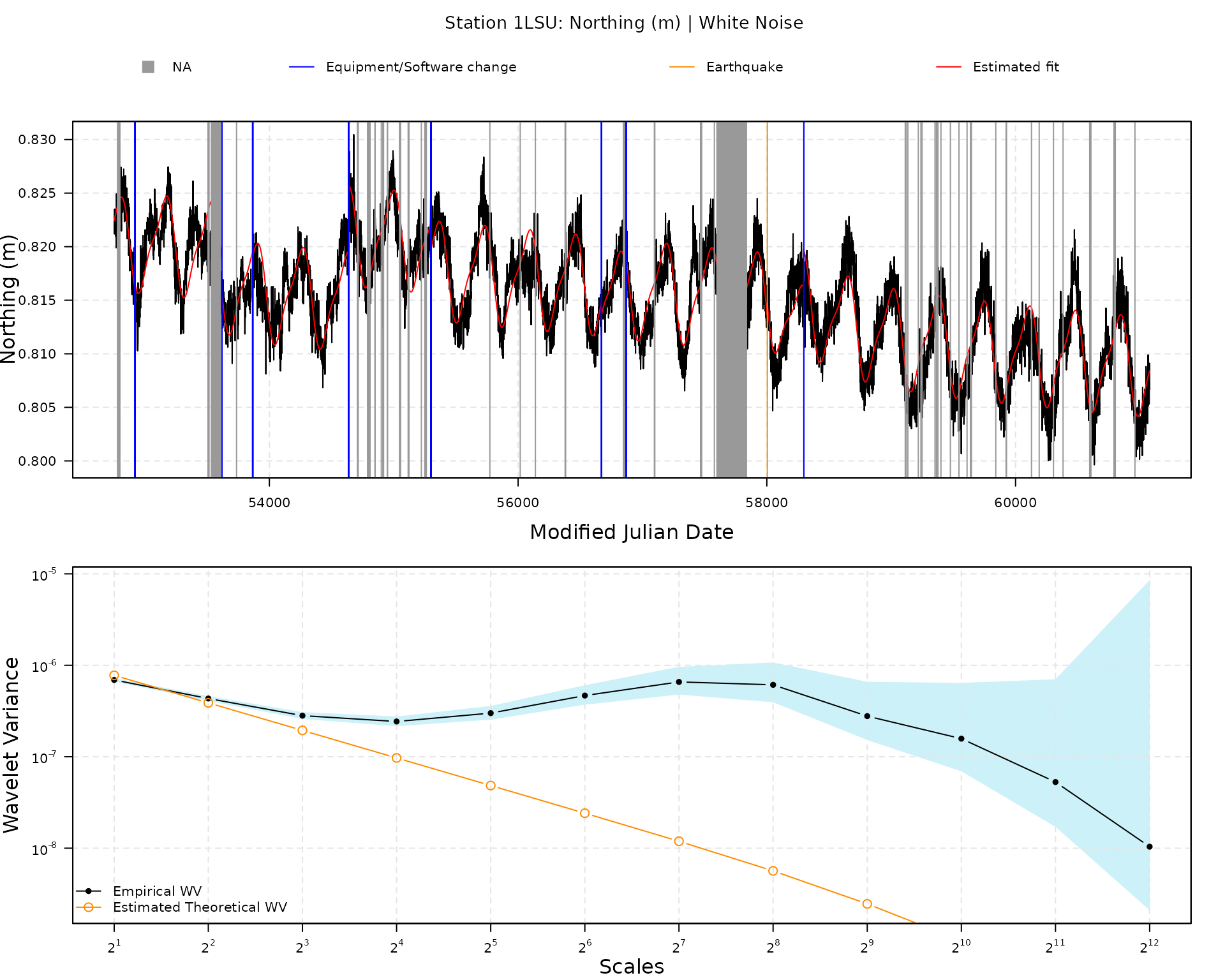

fit2 <- gmwmx2(station_data, n_seasonal = 2, component = "N", model = wn()+ pl())
fit2

## GMWMX fit GNSS Times Series (Nevada Geodetic Laboratory)
##                         Estimate Std.Error   CI.Lower  CI.Upper
## Intercept              8.156e-01 5.429e-01 -2.485e-01 1.880e+00
## Trend                 -1.090e-06 1.396e-05 -2.846e-05 2.628e-05
## Sin (Annual)          -5.216e-04 8.143e-03 -1.648e-02 1.544e-02
## Cos (Annual)          -4.129e-03 8.144e-03 -2.009e-02 1.183e-02
## Sin (Semi-Annual)      1.089e-03 7.825e-03 -1.425e-02 1.643e-02
## Cos (Semi-Annual)     -4.455e-04 7.824e-03 -1.578e-02 1.489e-02
## Jump: MJD 52920        4.958e-04 4.439e-02 -8.650e-02 8.749e-02
## Jump: MJD 53619       -3.057e-03 3.861e-02 -7.873e-02 7.262e-02
## Jump: MJD 53866       -5.586e-04 3.832e-02 -7.567e-02 7.455e-02
## Jump: MJD 54637       -2.499e-04 1.267e-01 -2.485e-01 2.480e-01
## Jump: MJD 54640        6.393e-03 1.267e-01 -2.420e-01 2.548e-01
## Jump: MJD 55300       -2.496e-03 2.835e-02 -5.805e-02 5.306e-02
## Jump: MJD 56671       -1.193e-03 4.077e-02 -8.110e-02 7.872e-02
## Jump: MJD 56868        1.120e-03 4.067e-02 -7.859e-02 8.083e-02
## Jump: MJD 58298        3.321e-03 6.656e-02 -1.271e-01 1.338e-01
## Jump: MJD 58004        1.137e-03 4.488e-02 -8.683e-02 8.911e-02
## Earthquake: MJD 58004 -7.135e-03 1.108e-01 -2.243e-01 2.101e-01
## 
## Missingness model
##   Proportion missing : 0.0584 
##   p1                 : 0.0073 
##   p2                 : 0.1173 
##   p*                 : 0.9416 
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 8.165e-07 
##   [2] Stationary PowerLaw
##        Estimated parameters : kappa =    -1, sigma2 = 9.708e-07 
## 
## Runtime (seconds)
##   Total              : 2.8893

plot(fit2)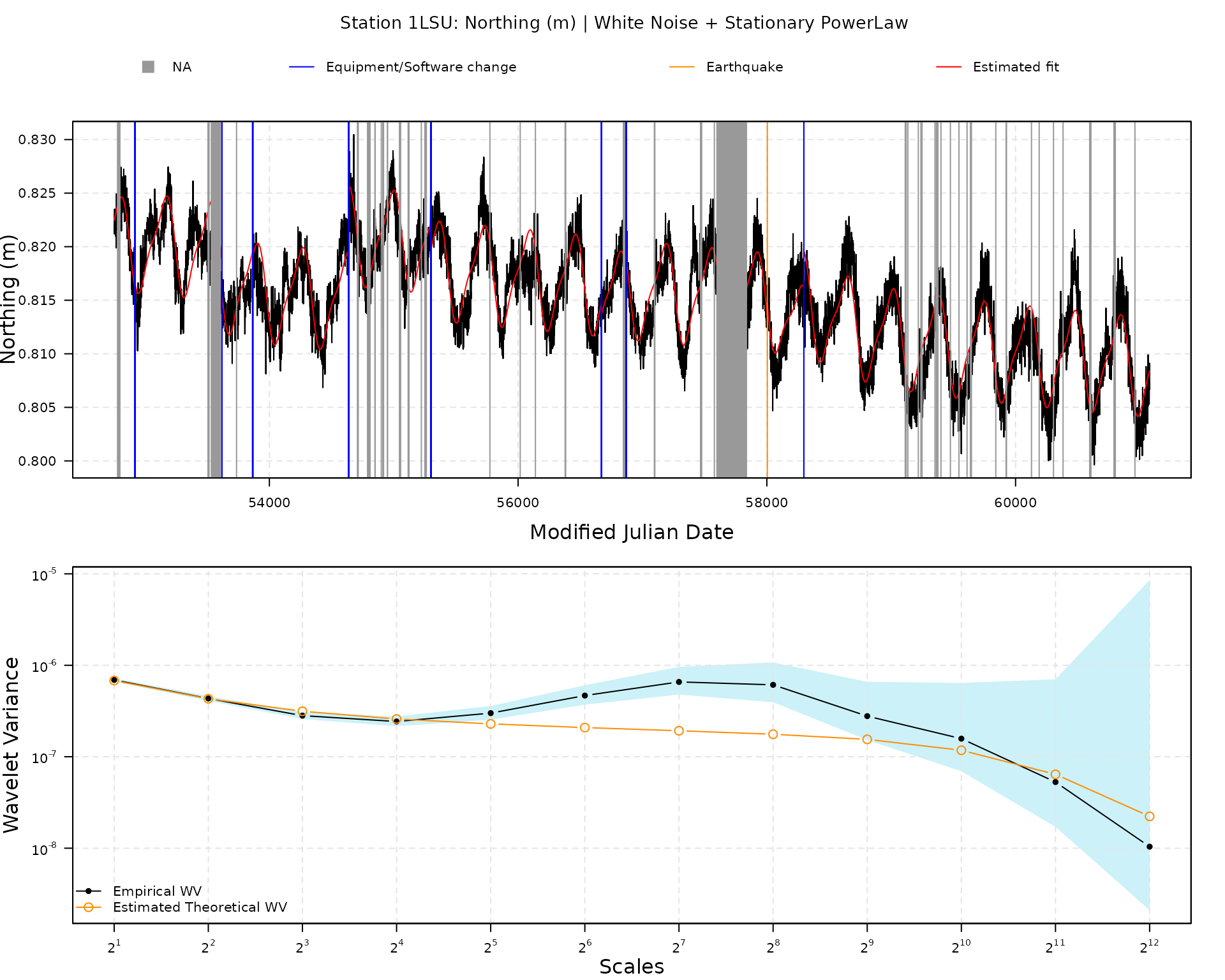

fit3 = gmwmx2(station_data, n_seasonal = 2, component = "N", model = wn() + flicker())
fit3

## GMWMX fit GNSS Times Series (Nevada Geodetic Laboratory)
##                         Estimate Std.Error   CI.Lower   CI.Upper
## Intercept              8.156e-01 2.298e-03  8.111e-01  8.201e-01
## Trend                 -1.090e-06 5.367e-07 -2.142e-06 -3.774e-08
## Sin (Annual)          -5.216e-04 1.246e-04 -7.659e-04 -2.773e-04
## Cos (Annual)          -4.129e-03 1.279e-04 -4.380e-03 -3.878e-03
## Sin (Semi-Annual)      1.089e-03 8.826e-05  9.160e-04  1.262e-03
## Cos (Semi-Annual)     -4.455e-04 8.823e-05 -6.184e-04 -2.725e-04
## Jump: MJD 52920        4.958e-04 9.597e-04 -1.385e-03  2.377e-03
## Jump: MJD 53619       -3.057e-03 1.001e-03 -5.019e-03 -1.095e-03
## Jump: MJD 53866       -5.586e-04 1.020e-03 -2.559e-03  1.441e-03
## Jump: MJD 54637       -2.499e-04 1.594e-03 -3.374e-03  2.875e-03
## Jump: MJD 54640        6.393e-03 1.581e-03  3.294e-03  9.492e-03
## Jump: MJD 55300       -2.496e-03 1.066e-03 -4.586e-03 -4.063e-04
## Jump: MJD 56671       -1.193e-03 1.114e-03 -3.377e-03  9.908e-04
## Jump: MJD 56868        1.120e-03 1.101e-03 -1.038e-03  3.279e-03
## Jump: MJD 58298        3.321e-03 1.458e-03  4.623e-04  6.179e-03
## Jump: MJD 58004        1.137e-03 1.493e-03 -1.790e-03  4.064e-03
## Earthquake: MJD 58004 -7.135e-03 3.175e-03 -1.336e-02 -9.126e-04
## 
## Missingness model
##   Proportion missing : 0.0584 
##   p1                 : 0.0073 
##   p2                 : 0.1173 
##   p*                 : 0.9416 
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 8.156e-07 
##   [2] Flicker
##        Estimated parameters : sigma2 = 9.725e-07 
## 
## Runtime (seconds)
##   Total              : 6.0101

plot(fit3)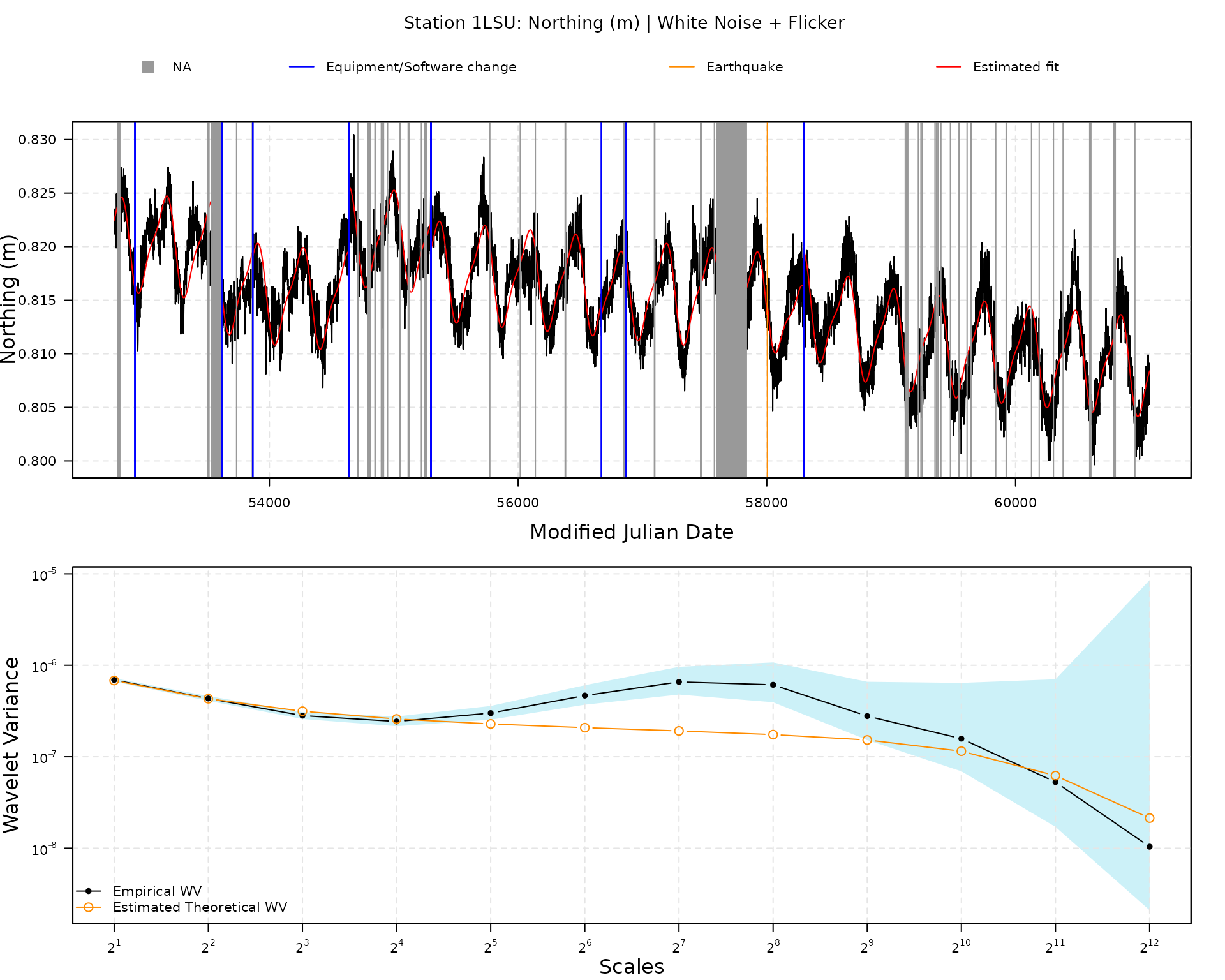

fit4 = gmwmx2(station_data, n_seasonal = 2, component = "N", model = wn() + ar1())
fit4

## GMWMX fit GNSS Times Series (Nevada Geodetic Laboratory)
##                         Estimate Std.Error   CI.Lower   CI.Upper
## Intercept              8.156e-01 2.265e-03  8.112e-01  8.200e-01
## Trend                 -1.090e-06 4.736e-07 -2.018e-06 -1.613e-07
## Sin (Annual)          -5.216e-04 2.248e-04 -9.623e-04 -8.096e-05
## Cos (Annual)          -4.129e-03 2.264e-04 -4.573e-03 -3.685e-03
## Sin (Semi-Annual)      1.089e-03 1.493e-04  7.964e-04  1.382e-03
## Cos (Semi-Annual)     -4.455e-04 1.494e-04 -7.384e-04 -1.526e-04
## Jump: MJD 52920        4.958e-04 1.369e-03 -2.187e-03  3.179e-03
## Jump: MJD 53619       -3.057e-03 1.254e-03 -5.514e-03 -5.996e-04
## Jump: MJD 53866       -5.586e-04 1.247e-03 -3.003e-03  1.886e-03
## Jump: MJD 54637       -2.499e-04 2.009e-03 -4.187e-03  3.687e-03
## Jump: MJD 54640        6.393e-03 2.010e-03  2.453e-03  1.033e-02
## Jump: MJD 55300       -2.496e-03 9.734e-04 -4.404e-03 -5.887e-04
## Jump: MJD 56671       -1.193e-03 1.302e-03 -3.745e-03  1.359e-03
## Jump: MJD 56868        1.120e-03 1.297e-03 -1.421e-03  3.661e-03
## Jump: MJD 58298        3.321e-03 1.969e-03 -5.392e-04  7.181e-03
## Jump: MJD 58004        1.137e-03 1.484e-03 -1.771e-03  4.045e-03
## Earthquake: MJD 58004 -7.135e-03 3.385e-03 -1.377e-02 -5.004e-04
## 
## Missingness model
##   Proportion missing : 0.0584 
##   p1                 : 0.0073 
##   p2                 : 0.1173 
##   p*                 : 0.9416 
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 1.434e-06 
##   [2] AR(1)
##        Estimated parameters : phi = 0.9803, sigma2 = 1.35e-07 
## 
## Runtime (seconds)
##   Total              : 2.3920

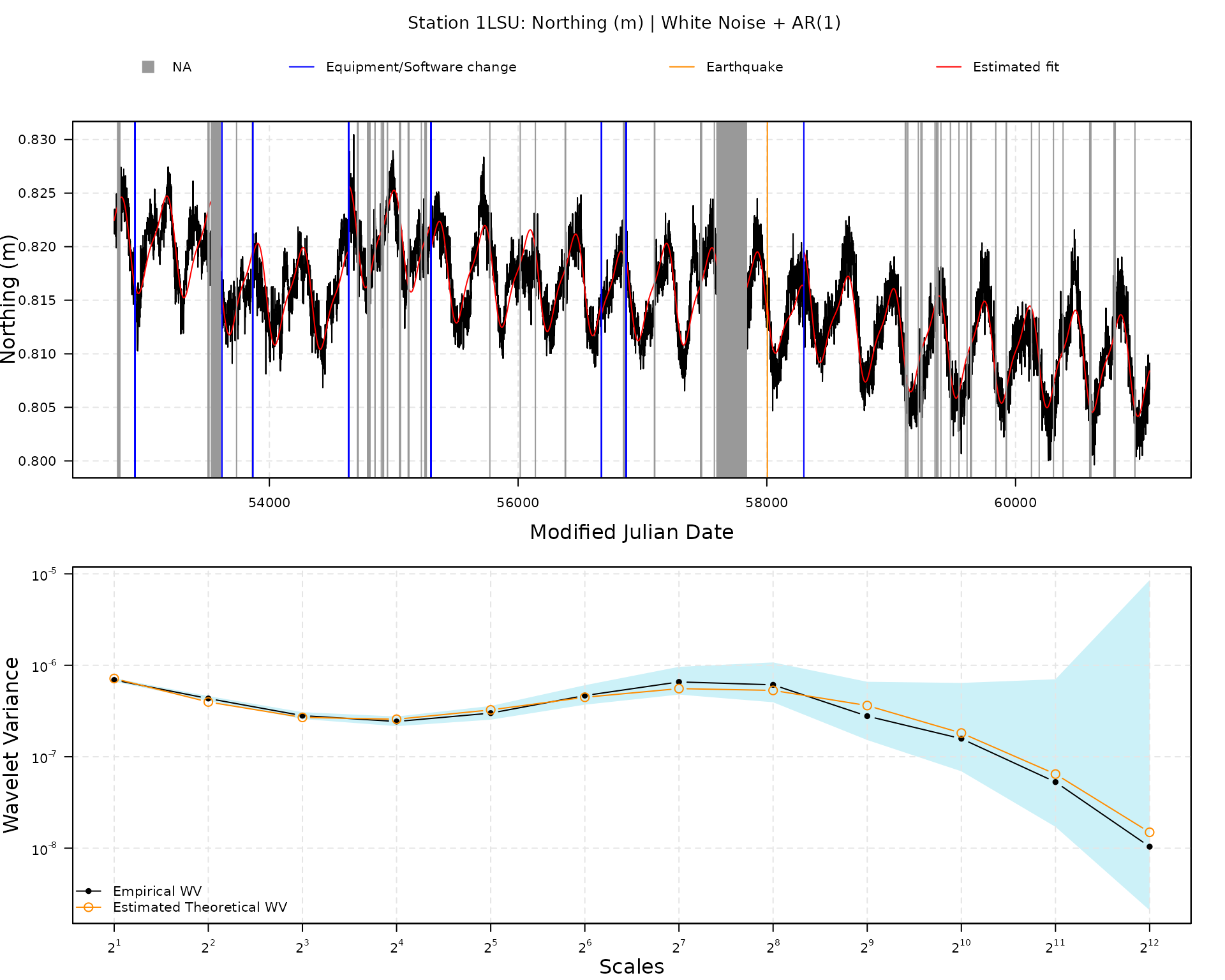
plot(fit4)

References

Bevis, Michael, and A. Brown. 2014. “Trajectory Models and Reference Frames for Crustal Motion Geodesy.” Journal of Geodesy 88 (283): 283--311.

Blewitt, Geoffrey. 2024. “An Improved Equation of Latitude and a Global System of Graticule Distance Coordinates.” Journal of Geodesy 98 (1): 6.

Blewitt, Geoffrey, William Hammond, and Corn Kreemer. 2018. “Harnessing the GPS Data Explosion for Interdisciplinary Science.” Eos 99 (2): e2020943118.

Bos, MS, RMS Fernandes, SDP Williams, and L Bastos. 2013. “Fast Error Analysis of Continuous GNSS Observations with Missing Data.” Journal of Geodesy 87 (4): 351–60.

He, Xiaoxing, Jean-Philippe Montillet, Rui Fernandes, Machiel Bos, Kegen Yu, Xianghong Hua, and Weiping Jiang. 2017. “Review of Current GPS Methodologies for Producing Accurate Time Series and their Error Sources.” Journal of Geodynamics 106: 12–29.

Langbein, John. 2008. “Noise in GPS Displacement Measurements from Southern California and Southern Nevada.” Journal of Geophysical Research: Solid Earth 113 (B5): 1–12.

Sobrero, Franco S, Michael Bevis, Demián D Gómez, and Fei Wang. 2020. “Logarithmic and Exponential Transients in GNSS Trajectory Models as Indicators of Dominant Processes in Postseismic Deformation.” Journal of Geodesy 94 (9): 84.

Voirol, Lionel, Haotian Xu, Yuming Zhang, Luca Insolia, Roberto Molinari, and Stéphane Guerrier. 2024. “Inference for Large Scale Regression Models with Dependent Errors.” arXiv Preprint arXiv:2409.05160.

Williams, Simon DP, Yehuda Bock, Peng Fang, Paul Jamason, Rosanne M Nikolaidis, Linette Prawirodirdjo, Meghan Miller, and Daniel J Johnson. 2004. “Error Analysis of Continuous GPS Position Time Series.” Journal of Geophysical Research: Solid Earth 109 (B3).