GMWMX: Estimate linear models with dependent errors

Source: vignettes/estimate_linear_models_with_dependent_errors.Rmd

This vignette demonstrates how to use the GMWMX estimator to estimate linear models with dependent errors described by a composite stochastic process. Consider the model defined as:

𝐘=𝐗𝛃+𝛆,π›†βˆΌβ„±{𝟎,𝚺(𝛄)},\begin{equation} \mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}, \quad \boldsymbol{\varepsilon} \sim \mathcal{F}\left\{\mathbf{0}, \boldsymbol{\Sigma}\left(\boldsymbol{\gamma}\right)\right\}, \end{equation}

where π—βˆˆβ„nΓ—p\mathbf{X} \in \mathbb{R}^{n \times p} is a design matrix of observed predictors, π›ƒβˆˆβ„p\boldsymbol{\beta} \in \mathbb{R}^p is the regression parameter vector and 𝛆={Ξ΅i}i=1,…,n\boldsymbol{\varepsilon} = \{\varepsilon_{i}\}_{i=1,\ldots,n} is a zero-mean process following an unspecified joint distribution β„±\mathcal{F} with positive-definite covariance function 𝚺(𝛄)βˆˆβ„nΓ—n\boldsymbol{\Sigma}(\boldsymbol{\gamma}) \in \mathbb{R}^{n\times n} characterizing the second-order dependence structure of the process and parameterized by the vector π›„βˆˆπšͺβŠ‚β„q\boldsymbol{\gamma} \in \boldsymbol{\Gamma} \subset \mathbb{R}^q.

The GMWMX estimator first estimates with the least-squares estimator:

𝛃̂=(𝐗T𝐗)βˆ’1𝐗T𝐘,\begin{equation} \hat{\boldsymbol{\beta}} = \left( \mathbf{X}^T \mathbf{X}\right)^{-1} \mathbf{X}^T \boldsymbol{Y}, \end{equation}

It then estimates the parameters of the stochastic model with a Generalized Method of Wavelet Moments approach (Guerrier et al. 2013) applied to the estimated residuals defined as 𝛆̂=π˜βˆ’π—π›ƒΜ‚\hat{\boldsymbol{\varepsilon}} = {\boldsymbol{Y}} - { \mathbf{X}} \hat{\boldsymbol{\beta}}.

More precisely, the estimated stochastic parameters, denoted as 𝛄̂\hat{\boldsymbol{\gamma}}, are defined as:

𝛄̂=argminπ›„βˆˆπšͺ{π›ŽΜ‚βˆ’π›Ž(𝛄)}T𝛀{π›ŽΜ‚βˆ’π›Ž(𝛄)},\begin{equation} \hat{\boldsymbol{\gamma}} = \underset{\boldsymbol{\gamma} \in \boldsymbol{\Gamma}}{\arg\min} \left\{\hat{\boldsymbol{\nu}} - \boldsymbol{\nu}(\boldsymbol{\gamma})\right\}^T \boldsymbol{\Omega} \left\{\hat{\boldsymbol{\nu}} - \boldsymbol{\nu}(\boldsymbol{\gamma})\right\}, \end{equation}

where π›ŽΜ‚\hat{\boldsymbol{\nu}} is the vector of empirical wavelet variances computed on the estimated residuals 𝛆̂\hat{\boldsymbol{\varepsilon}}, π›Ž(𝛄)\boldsymbol{\nu}(\boldsymbol{\gamma}) is the vector of theoretical wavelet variance implied by the stochastic model with parameters 𝛄\boldsymbol{\gamma}, and 𝛀\boldsymbol{\Omega} is a weighting matrix.

The theoretical wavelet variance π›Ž(𝛄)\boldsymbol{\nu}(\boldsymbol{\gamma}) is obtained using the results of Xu et al. (2017) and Zhang (2008) that provide a computationally efficient form of the theoretical Allan variance (equivalent to the Haar wavelet variance up to a constant) for zero-mean stochastic processes such as 𝛆\boldsymbol{\varepsilon}. In Xu et al. (2017) they generalize the results in Zhang (2008) to zero-mean non-stationary processes by using averages of the diagonals and super-diagonals of the covariance matrix of 𝛆\boldsymbol{\varepsilon}. This implies that GMWMX does not require storage of the nΓ—nn \times n covariance matrix of 𝛆\boldsymbol{\varepsilon}, but only a vector of length nn that is plugged into an explicit formula consisting of a linear combination of its elements.

The variance-covariance matrix of the estimated regression parameters 𝛃̂\hat{\boldsymbol{\beta}} is then obtained as:

(π—βŠ€π—)βˆ’1π—βŠ€πšΊ(𝛄̂)𝐗(π—βŠ€π—)βˆ’1.\begin{equation} (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} {\boldsymbol{\Sigma}}(\hat{\boldsymbol{\gamma}}) \mathbf{X} (\mathbf{X}^{\top} \mathbf{X})^{-1}. \end{equation}

This vignette is a detailed, self-contained simulation walkthrough that showcases gmwmx2() for an arbitrary design matrix X and response vector y. We build the signal, generate noise, fit models, and run Monte Carlo experiments to check coverage of confidence intervals. For each setting, we also plot the empirical distributions of the estimated functional and stochastic parameters.

library(gmwmx2)
library(wv)
library(dplyr)

boxplot_mean_dot <- function(x, ...) {
  boxplot(x, ...)
  x_mat <- as.matrix(x)
  mean_vals <- colMeans(x_mat, na.rm = TRUE)
  points(seq_along(mean_vals), mean_vals, pch = 16, col = "black")
}

Build an arbitrary design matrix X

We use a generic design matrix that mirrors many geodetic or environmental signals:

  1. Intercept.
  2. Linear trend.
  3. Annual sinusoid and cosine.

This is arbitrary and can be replaced with any design matrix suitable to your application.

n = 15*365 
X = matrix(NA, nrow = n, ncol = 4)
# intercept
X[, 1] = 1
# trend
X[, 2] = 1:n
# annual sinusoid
omega_1 <- (1 / 365.25) * 2 * pi
X[, 3] <- sin((1:n) * omega_1)
X[, 4] <- cos((1:n) * omega_1)
beta = c(0.5 , 0.00004, 0.005,  0.0008)


# visualize the deterministic signal
plot(x = X[, 2], y = X %*% beta, type = "l",
     main = "Signal", xlab = "Time", ylab = "Signal", las = 1)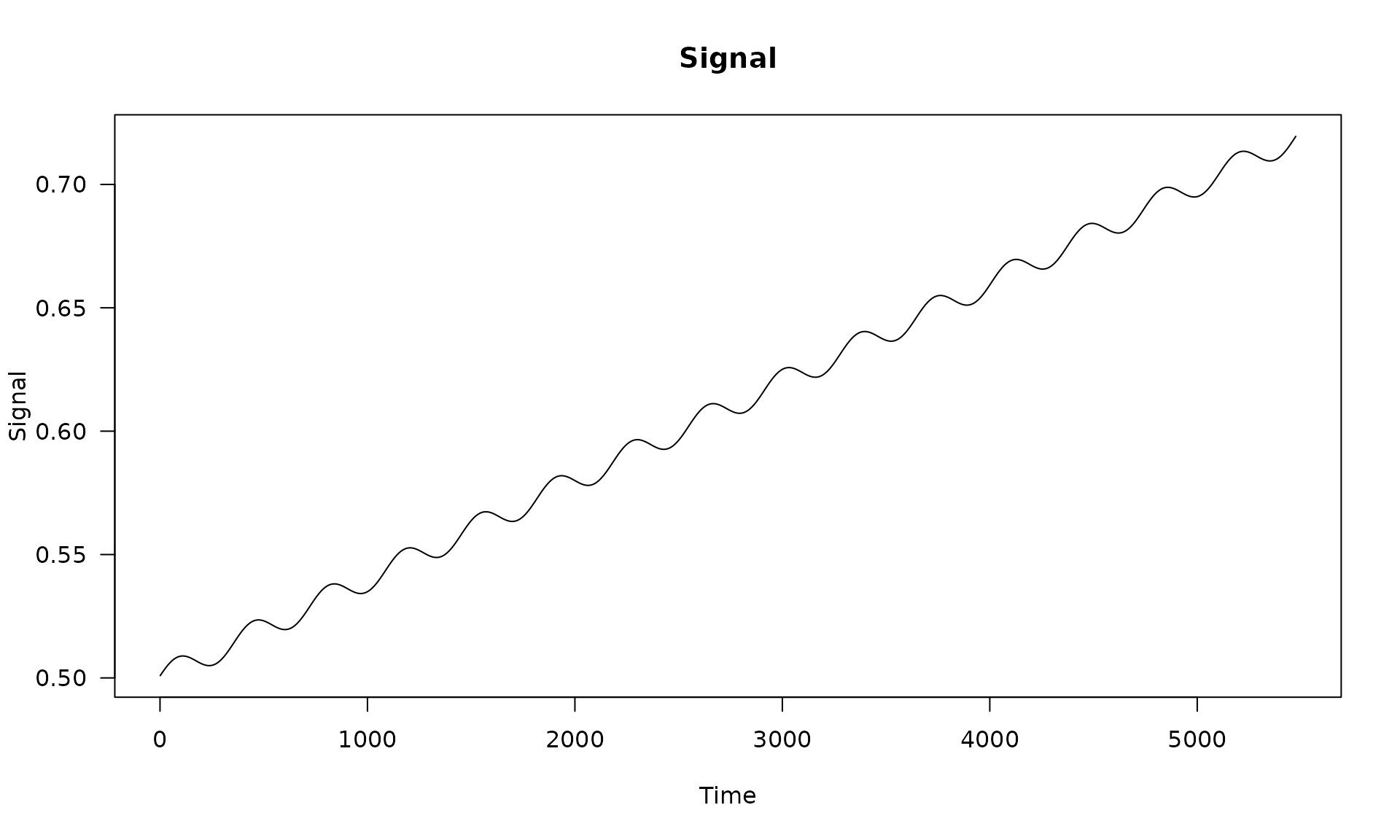

We now define three different stochastic noise settings using the same X and beta.

Example 1: White noise + AR(1)

Generate signal 

phi_ar1 = 0.975
sigma2_ar1 =  5e-05
sigma2_wn =  7e-04
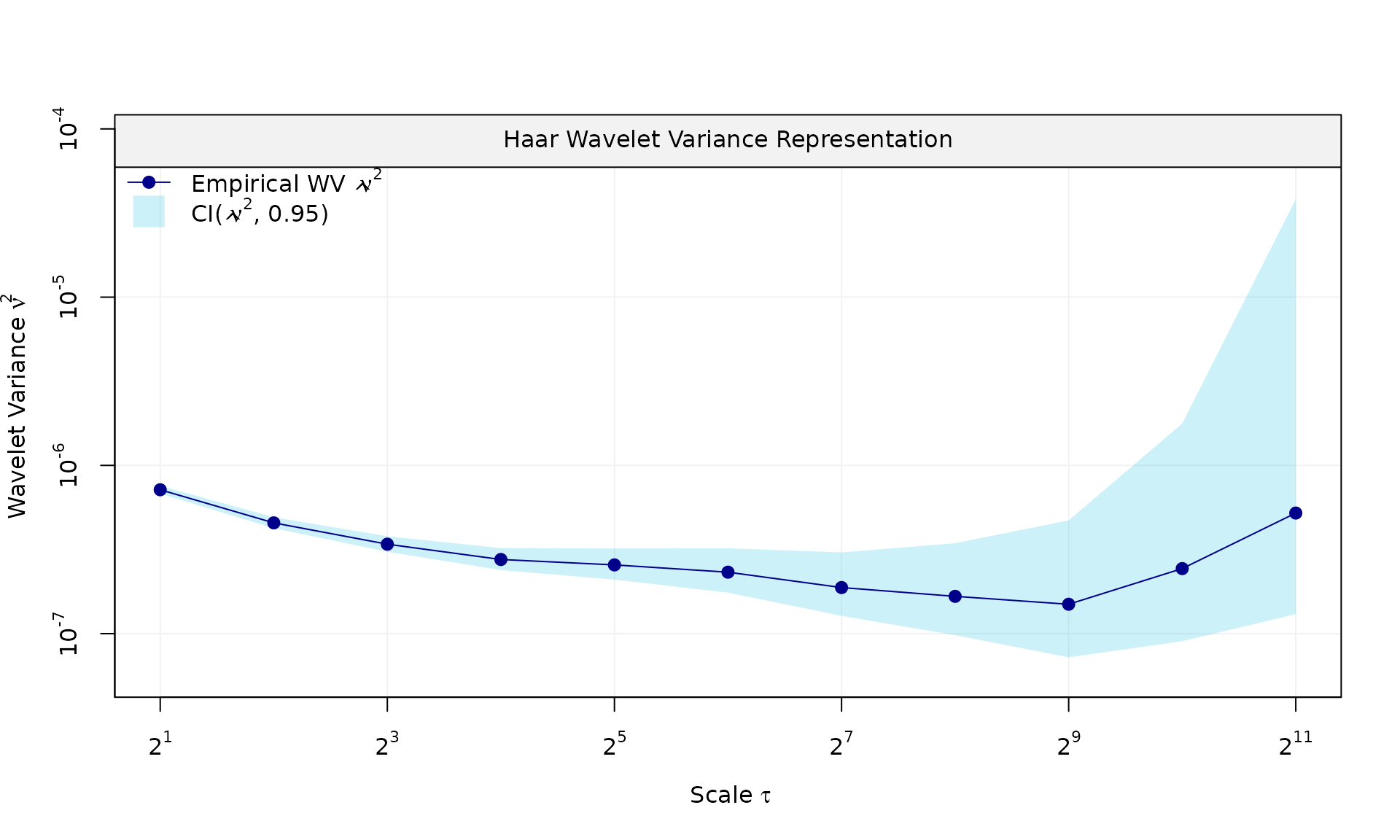
eps = gmwmx2::generate(ar1(phi = phi_ar1, sigma2 = sigma2_ar1) + wn(sigma2_wn), n = n, seed = 123)$series
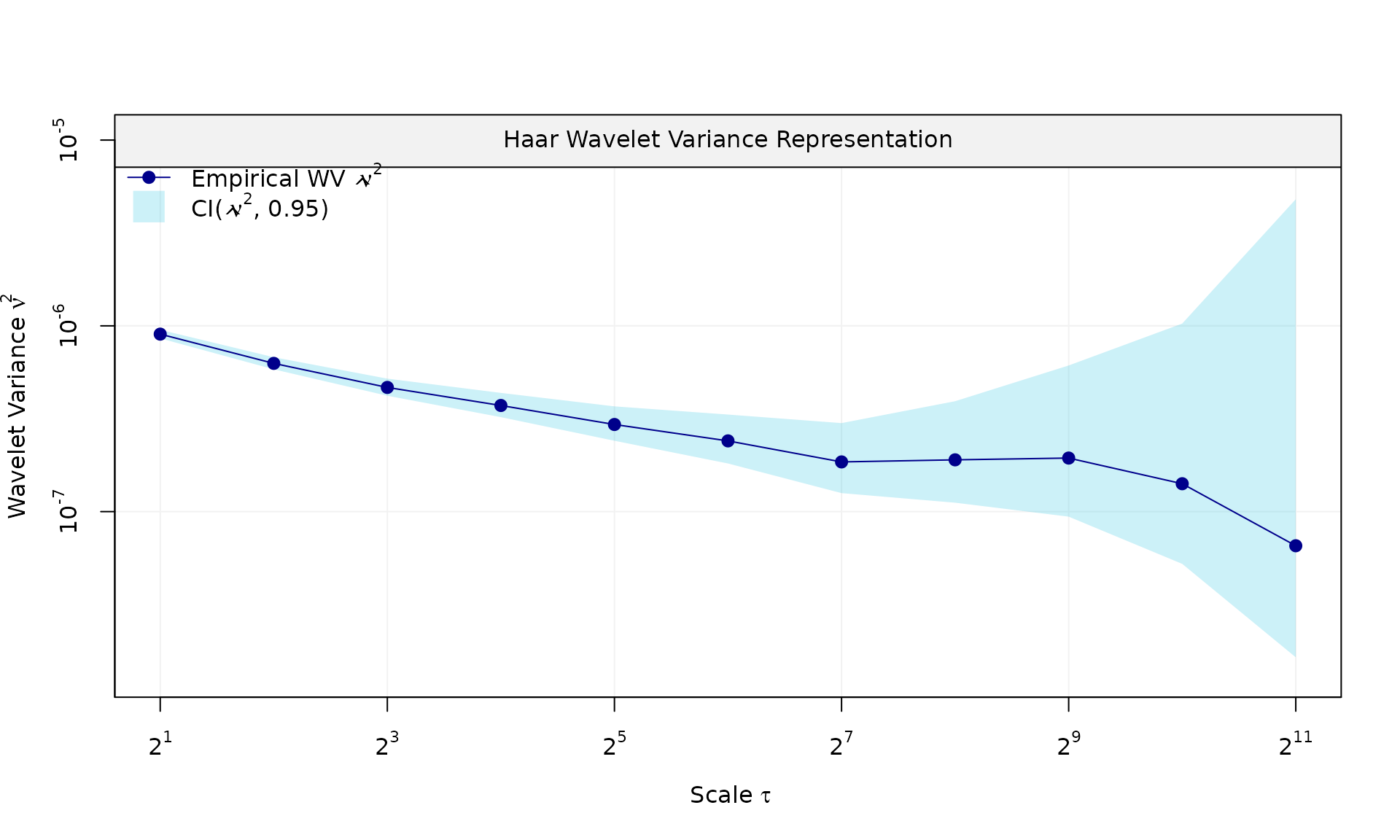
plot(wv::wvar(eps))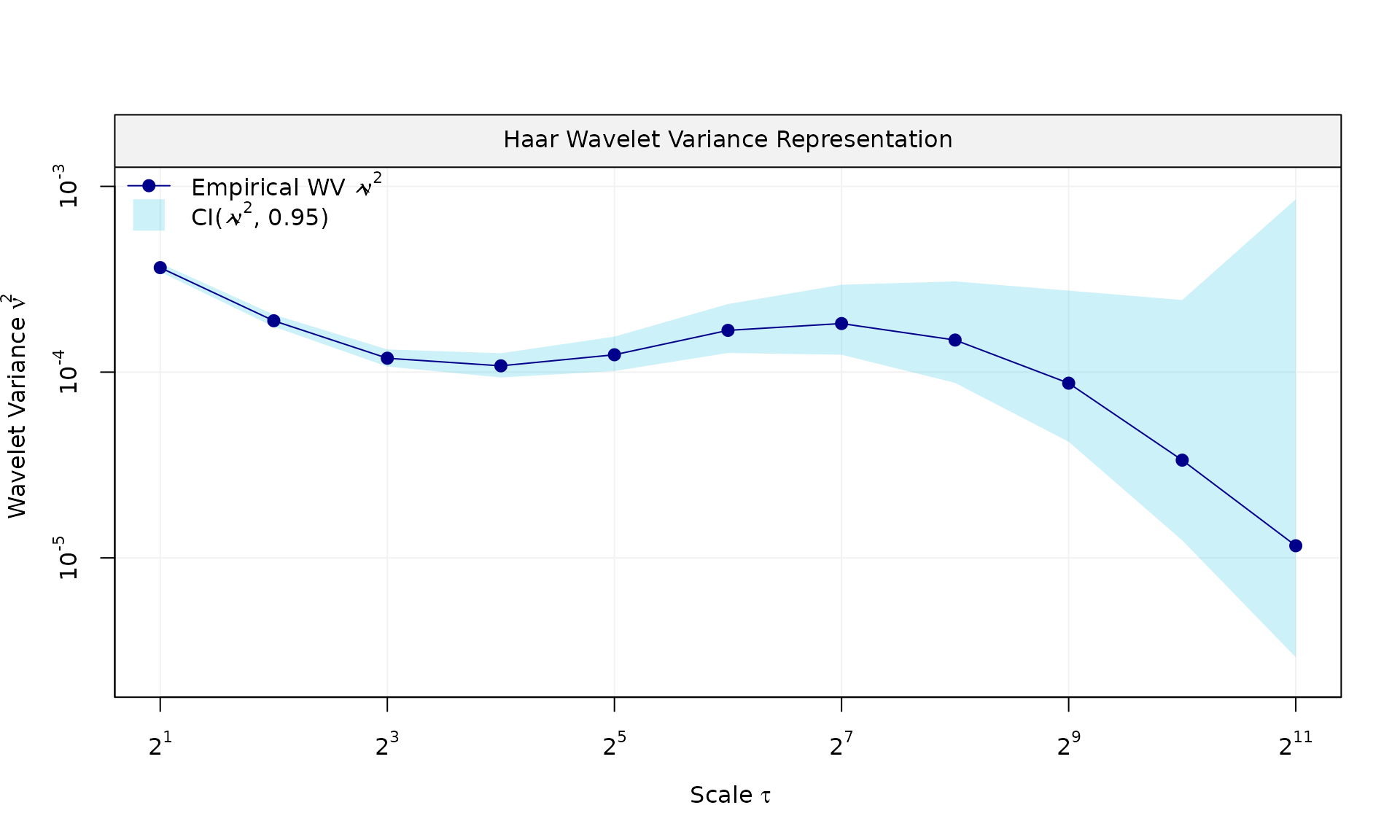

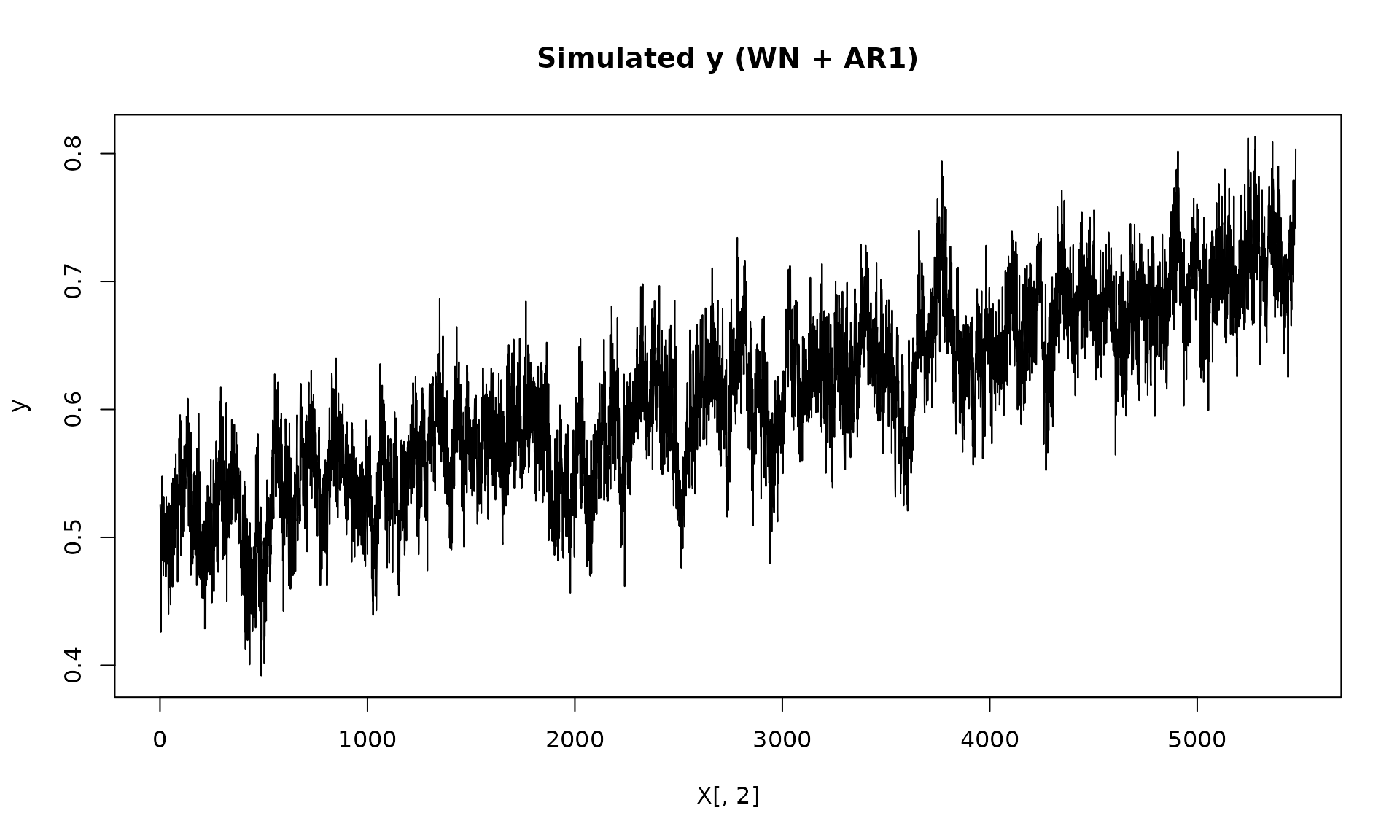
y = X %*% beta + eps
plot(X[, 2], y, type = "l", main = "Simulated y (WN + AR1)")

Fit model

We fit using gmwmx2() with a composite model composed of white noise and autoregressive process of order 1.

fit = gmwmx2(X = X, y = y, model = wn() + ar1() )
print(fit)
## GMWMX fit
##         Estimate Std.Error
## beta1  0.5055257 6.619e-03
## beta2  0.0000381 2.091e-06
## beta3  0.0049642 4.115e-03
## beta4 -0.0049813 4.088e-03
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 0.0006936 
##   [2] AR(1)
##        Estimated parameters : phi = 0.9701, sigma2 = 5.367e-05 
## 
## Runtime (seconds)
##   Total              : 2.3833

To assess uncertainty, we run a Monte Carlo simulation and check empirical coverage of the confidence intervals for the trend.

Monte Carlo simulation 

B = 100
mat_res = matrix(NA, nrow=B, ncol=19)
for(b in seq(B)){
  eps = generate(ar1(phi=phi_ar1, sigma2=sigma2_ar1) + wn(sigma2_wn), n=n, seed = (123 + b))$series
  y = X %*% beta + eps
  fit = gmwmx2(X = X, y = y, model = wn() + ar1() )
  # misspecified model assuming white noise as the stochastic model
  fit2 = lm(y~X[,2] + X[,3] + X[,4])

  mat_res[b, ] = c(fit$beta_hat, fit$std_beta_hat,
                   summary(fit2)$coefficients[,1],
                   summary(fit2)$coefficients[,2],
                   fit$theta_domain$`AR(1)_2`,
                   fit$theta_domain$`White Noise_1`)
  # cat("Iteration ", b, " completed.\n")
}
# compute empirical coverage
mat_res_df = as.data.frame(mat_res)
colnames(mat_res_df) = c("gmwmx_beta0_hat", "gmwmx_beta1_hat",
                         "gmwmx_beta2_hat", "gmwmx_beta3_hat",
                         "gmwmx_std_beta0_hat", "gmwmx_std_beta1_hat",
                         "gmwmx_std_beta2_hat", "gmwmx_std_beta3_hat",
                         "lm_beta0_hat", "lm_beta1_hat", "lm_beta2_hat", "lm_beta3_hat",
                         "lm_std_beta0_hat", "lm_std_beta1_hat", "lm_std_beta2_hat", "lm_std_beta3_hat",
                         "phi_ar1","sigma_2_ar1" ,"sigma_2_wn")

Plot empirical distributions of estimated parameters 

par(mfrow = c(1, 4))
boxplot_mean_dot(mat_res_df[, c("gmwmx_beta0_hat")],las=1,
        names = c("beta0"),
        main = expression(beta[0]), ylab = "Estimate")
abline(h = beta[1], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta1_hat")],las=1,
        names = c("beta1"),
        main = expression(beta[1]), ylab = "Estimate")
abline(h = beta[2], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta2_hat")],las=1,
        names = c("beta2"),
        main = expression(beta[2]), ylab = "Estimate")
abline(h = beta[3], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta3_hat")],las=1,
        names = c("beta3"),
        main = expression(beta[3]), ylab = "Estimate")
abline(h = beta[4], col = "black", lwd = 2)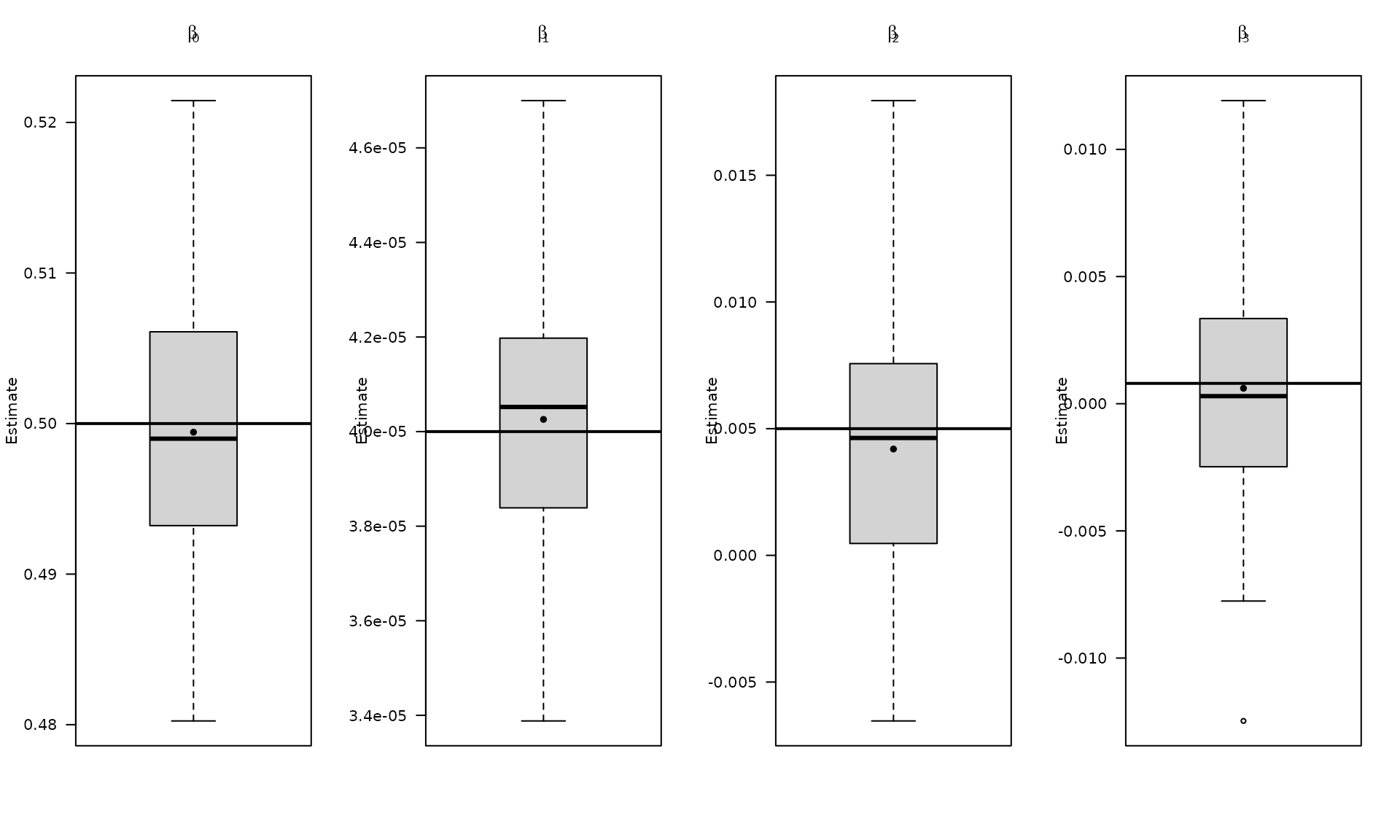

par(mfrow = c(1, 3))

boxplot_mean_dot(mat_res_df$phi_ar1,las=1,
        names = c("phi_ar1"),
        main = expression(phi["AR1"]), ylab = "Estimate")
abline(h = phi_ar1, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df$sigma_2_ar1,las=1,
        names = c("phi_ar1"),
        main = expression(sigma["AR1"]^2), ylab = "Estimate")
abline(h = sigma2_ar1, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df$sigma_2_wn,las=1,
        names = c("phi_ar1"),
        main = expression(sigma["WN"]^2), ylab = "Estimate")
abline(h = sigma2_wn, col = "black", lwd = 2)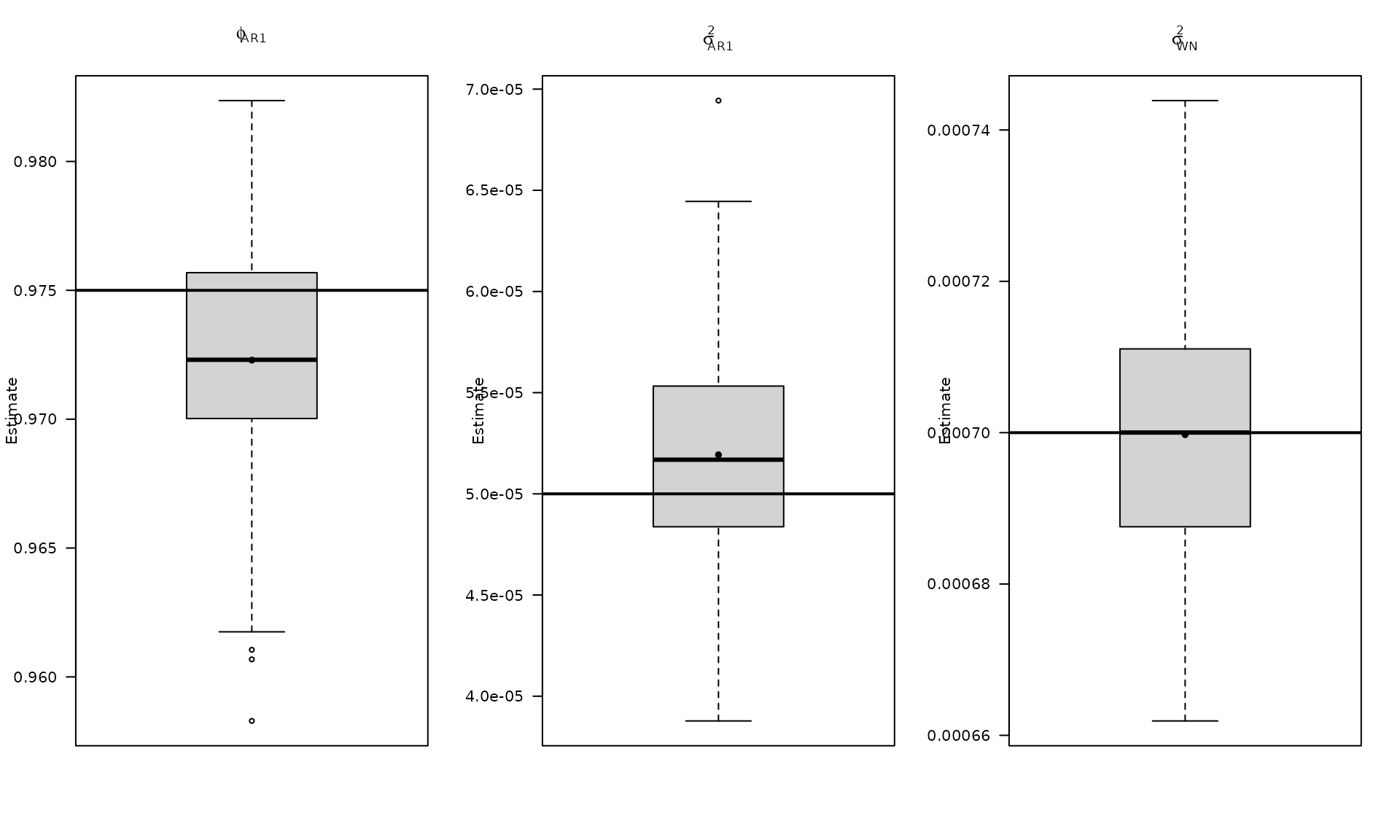

par(mfrow = c(1, 1))

Compute empirical coverage of confidence intervals 

zval = qnorm(0.975)
mat_res_df$upper_ci_gmwmx_beta1 = mat_res_df$gmwmx_beta1_hat + zval * mat_res_df$gmwmx_std_beta1_hat
mat_res_df$lower_ci_gmwmx_beta1 = mat_res_df$gmwmx_beta1_hat - zval * mat_res_df$gmwmx_std_beta1_hat
# empirical coverage of gmwmx beta
dplyr::between(rep(beta[2], B), mat_res_df$lower_ci_gmwmx_beta1, mat_res_df$upper_ci_gmwmx_beta1) %>% mean()
## [1] 0.87
# do the same for lm beta
mat_res_df$upper_ci_lm_beta1 = mat_res_df$lm_beta1_hat + zval * mat_res_df$lm_std_beta1_hat
mat_res_df$lower_ci_lm_beta1 = mat_res_df$lm_beta1_hat - zval * mat_res_df$lm_std_beta1_hat
dplyr::between(rep(beta[2], B), mat_res_df$lower_ci_lm_beta1, mat_res_df$upper_ci_lm_beta1) %>% mean()
## [1] 0.16

Example 2: White noise + stationary power-law

Generate signal

Here we replace AR(1) by a stationary power-law component.

kappa_pl <- -0.75
sigma2_wn <- 2e-07
sigma2_pl <- 2.25e-06
eps_pl = generate(wn(sigma2_wn) + pl(kappa = kappa_pl, sigma2 = sigma2_pl),
                  n = n, seed = 123)
plot(eps_pl$series, type = "l")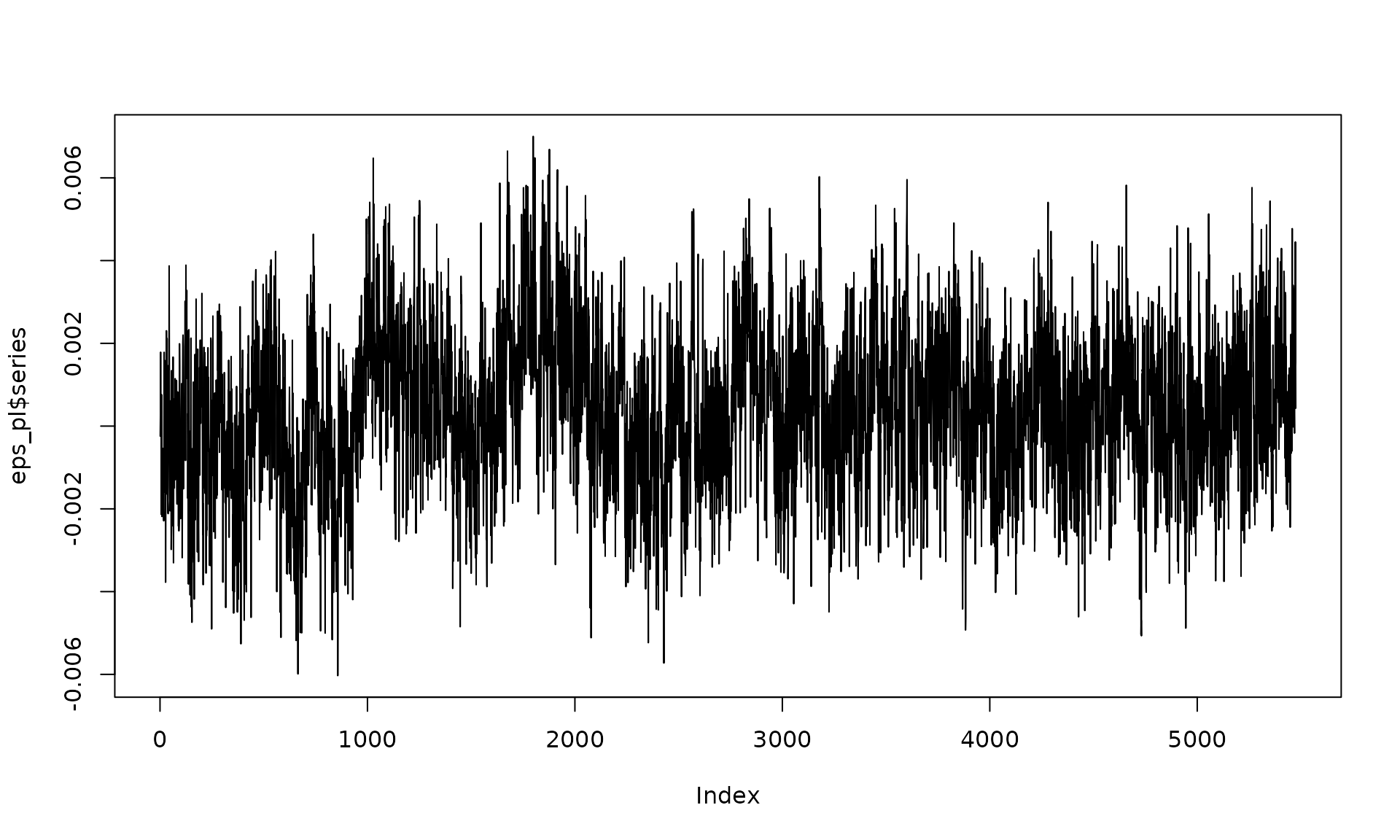

plot(wv::wvar(eps_pl$series))

y_pl = X %*% beta + eps_pl$series
plot(X[, 2], y_pl, type = "l", main = "Simulated y (WN + PL)")

Fit model 

fit_pl = gmwmx2(X = X, y = y_pl, model = wn() + pl())
fit_pl
## GMWMX fit
##        Estimate Std.Error
## beta1 5.002e-01 7.046e-04
## beta2 4.006e-05 1.662e-07
## beta3 4.787e-03 1.287e-04
## beta4 7.258e-04 1.269e-04
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 2.1e-13 
##   [2] Stationary PowerLaw
##        Estimated parameters : kappa = -0.7057, sigma2 = 2.52e-06 
## 
## Runtime (seconds)
##   Total              : 1.2013

Monte Carlo simulation 

B_pl = 100
mat_res_pl = matrix(NA, nrow = B_pl, ncol = 19)
for(b in seq(B_pl)){
  eps = generate(wn(sigma2_wn) + pl(kappa = kappa_pl, sigma2 = sigma2_pl),
                 n = n, seed = (123 + b))$series
  y = X %*% beta + eps
  fit = gmwmx2(X = X, y = y, model = wn() + pl())
  fit2 = lm(y~X[,2] + X[,3] + X[,4])

  mat_res_pl[b, ] = c(fit$beta_hat, fit$std_beta_hat,
                      summary(fit2)$coefficients[,1],
                      summary(fit2)$coefficients[,2],
                      fit$theta_domain$`Stationary PowerLaw_2`,
                      fit$theta_domain$`White Noise_1`)
  # cat("Iteration ", b, " \n")
}

mat_res_pl_df = as.data.frame(mat_res_pl)
colnames(mat_res_pl_df) = c("gmwmx_beta0_hat", "gmwmx_beta1_hat",
                            "gmwmx_beta2_hat", "gmwmx_beta3_hat",
                            "gmwmx_std_beta0_hat", "gmwmx_std_beta1_hat",
                            "gmwmx_std_beta2_hat", "gmwmx_std_beta3_hat",
                            "lm_beta0_hat", "lm_beta1_hat", "lm_beta2_hat", "lm_beta3_hat",
                            "lm_std_beta0_hat", "lm_std_beta1_hat",
                            "lm_std_beta2_hat", "lm_std_beta3_hat",
                            "kappa_pl","sigma2_pl" ,"sigma2_wn")

Plot empirical distributions of estimated parameters 

par(mfrow = c(1, 4))
boxplot_mean_dot(mat_res_df[, c("gmwmx_beta0_hat")],las=1,
        names = c("beta0"),
        main = expression(beta[0]), ylab = "Estimate")
abline(h = beta[1], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta1_hat")],las=1,
        names = c("beta1"),
        main = expression(beta[1]), ylab = "Estimate")
abline(h = beta[2], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta2_hat")],las=1,
        names = c("beta2"),
        main = expression(beta[2]), ylab = "Estimate")
abline(h = beta[3], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta3_hat")],las=1,
        names = c("beta3"),
        main = expression(beta[3]), ylab = "Estimate")
abline(h = beta[4], col = "black", lwd = 2)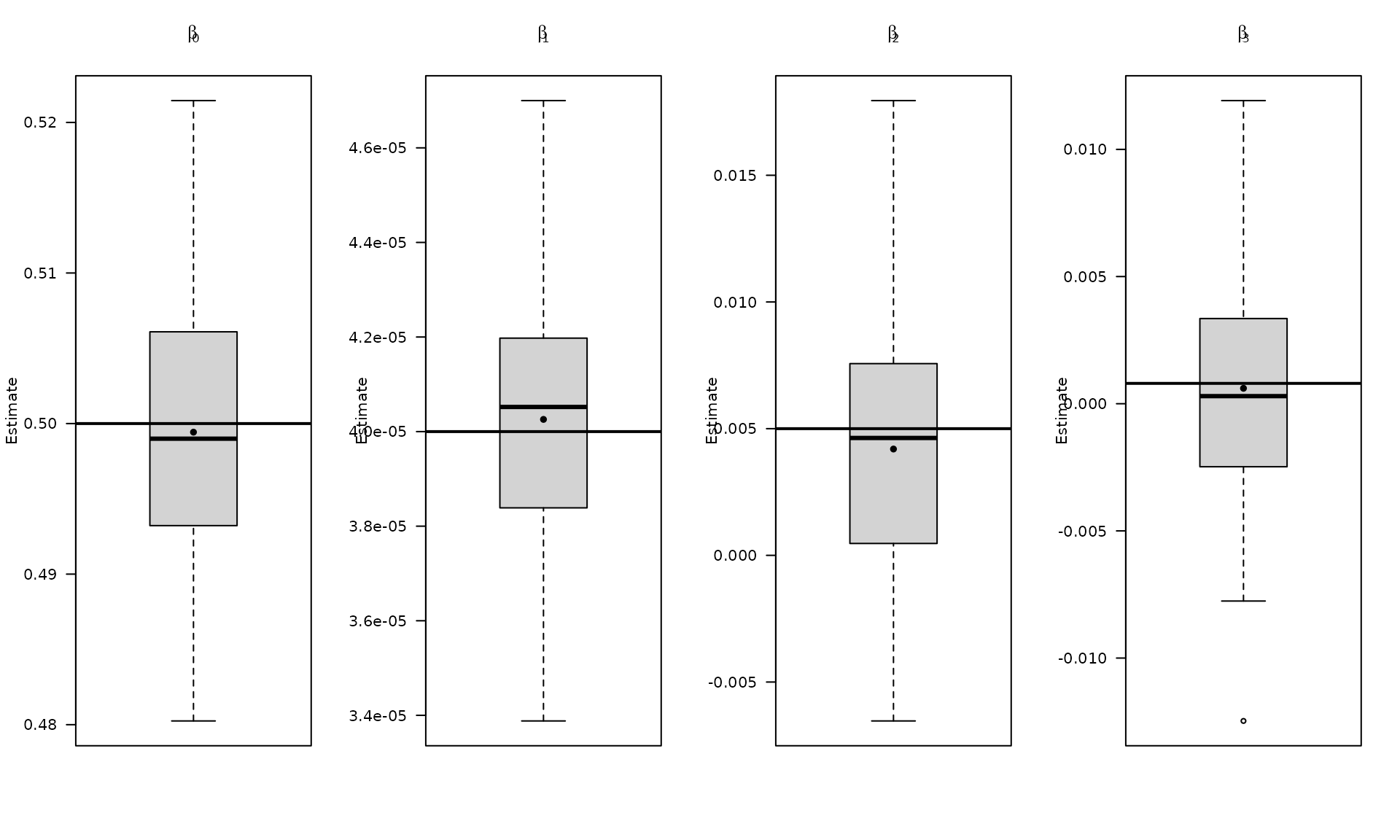

par(mfrow = c(1, 1))
par(mfrow = c(1, 3))

boxplot_mean_dot(mat_res_pl_df$kappa_pl,las=1,
        main = expression(kappa["PL"]), ylab = "Estimate")
abline(h = kappa_pl, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_pl_df$sigma2_pl,las=1,
        main = expression(sigma["PL"]^2), ylab = "Estimate")
abline(h = sigma2_pl, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_pl_df$sigma2_wn,las=1,
        names = c("phi_ar1"),
        main = expression(sigma["WN"]^2), ylab = "Estimate")
abline(h = sigma2_wn, col = "black", lwd = 2)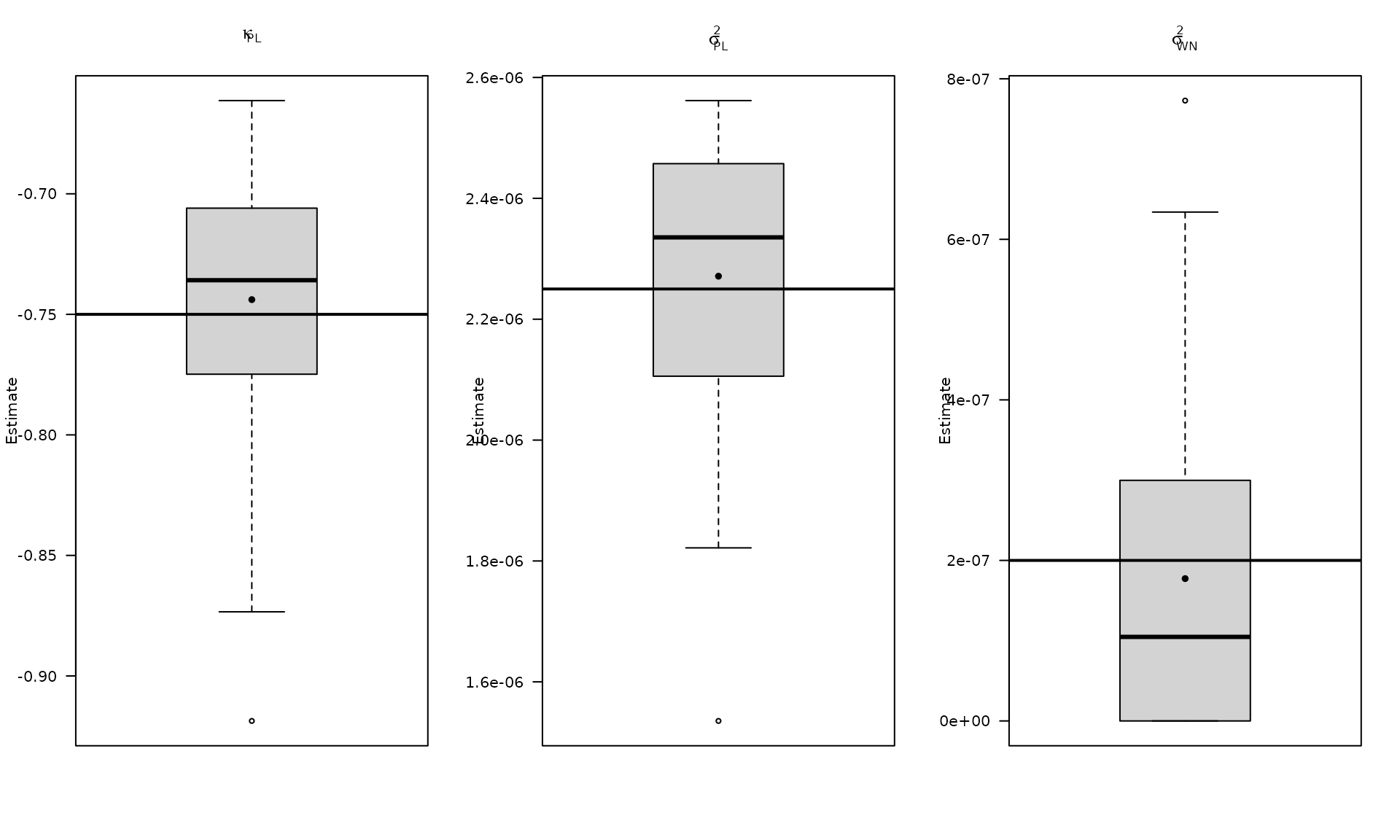

par(mfrow = c(1, 1))

Compute empirical coverage of confidence intervals 

zval = qnorm(0.975)
mat_res_pl_df$upper_ci_gmwmx_beta1 = mat_res_pl_df$gmwmx_beta1_hat + zval * mat_res_pl_df$gmwmx_std_beta1_hat
mat_res_pl_df$lower_ci_gmwmx_beta1 = mat_res_pl_df$gmwmx_beta1_hat - zval * mat_res_pl_df$gmwmx_std_beta1_hat
# empirical coverage of gmwmx beta
dplyr::between(rep(beta[2], B_pl), mat_res_pl_df$lower_ci_gmwmx_beta1, mat_res_pl_df$upper_ci_gmwmx_beta1) %>% mean()
## [1] 0.92
# do the same for lm beta
mat_res_pl_df$upper_ci_lm_beta1 = mat_res_pl_df$lm_beta1_hat + zval * mat_res_pl_df$lm_std_beta1_hat
mat_res_pl_df$lower_ci_lm_beta1 = mat_res_pl_df$lm_beta1_hat - zval * mat_res_pl_df$lm_std_beta1_hat
dplyr::between(rep(beta[2], B_pl), mat_res_pl_df$lower_ci_lm_beta1, mat_res_pl_df$upper_ci_lm_beta1) %>% mean()
## [1] 0.2

Example 3: White noise + flicker

Flicker noise corresponds to a non stationary power-law with spectral index ΞΊ=βˆ’1\kappa = -1 but is handled explicitly by flicker() in this package.

Generate signal 

# fix stochastic parameters
sigma2_wn_fl <- 8e-07
sigma2_fl <- 1e-06
eps_fl = generate(wn(sigma2_wn_fl) + flicker(sigma2 = sigma2_fl),
                  n = n, seed = 123)
plot(eps_fl$series, type = "l")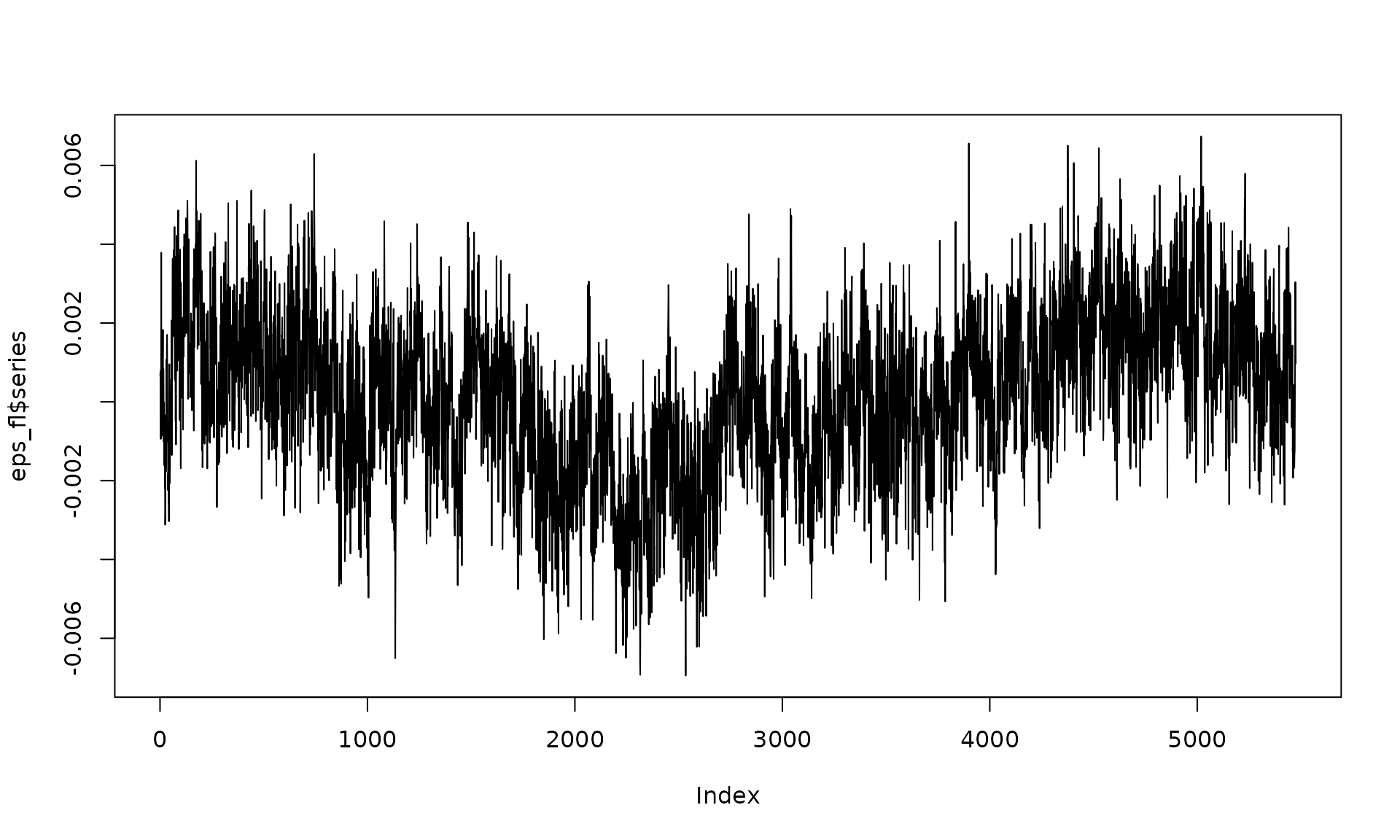

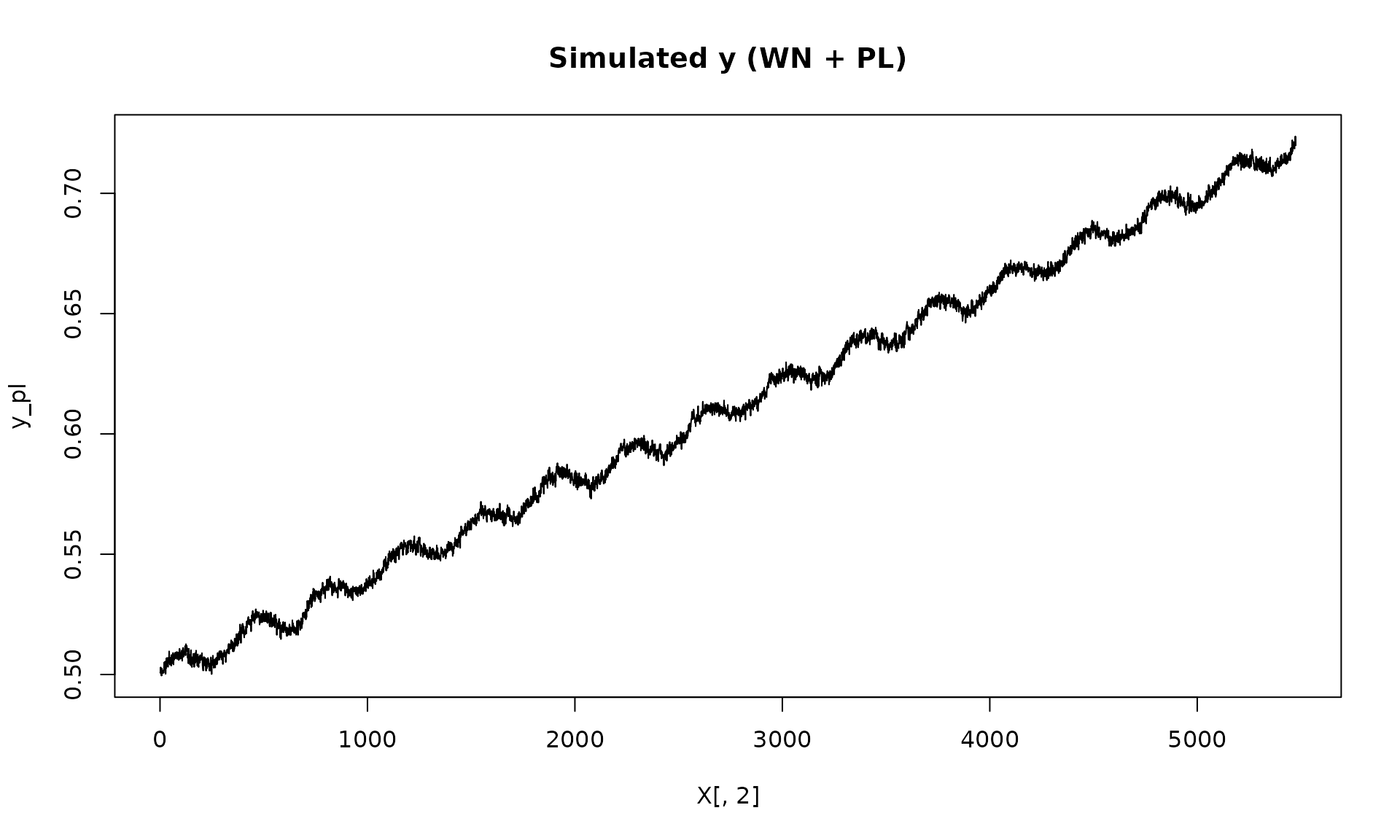
plot(wv::wvar(eps_fl$series))

y_fl = X %*% beta + eps_fl$series
plot(X[, 2], y_fl, type = "l", main = "Simulated y (WN + Flicker)")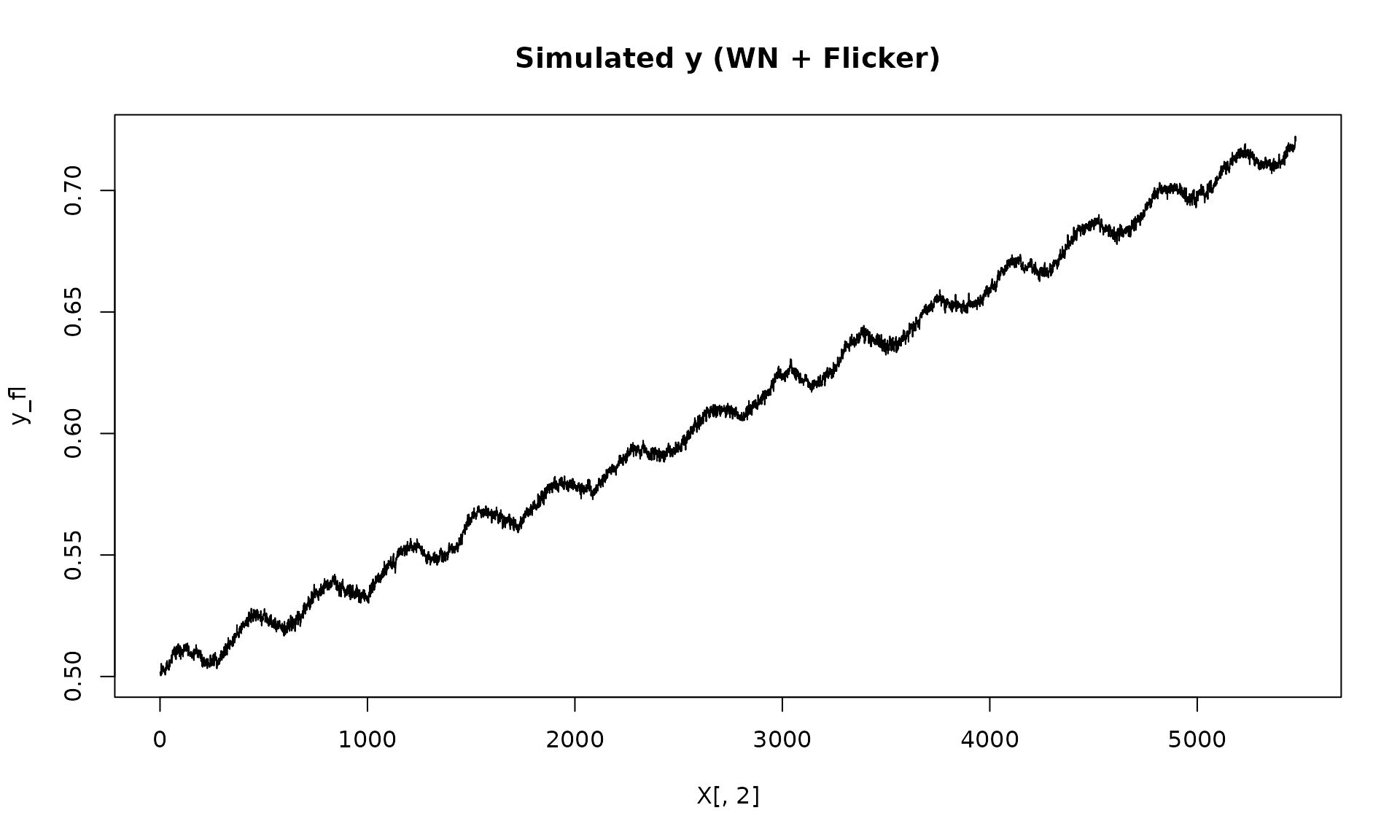

Fit model 

fit_fl = gmwmx2(X = X, y = y_fl, model = wn() + flicker())
fit_fl
## GMWMX fit
##        Estimate Std.Error
## beta1 4.995e-01 9.257e-04
## beta2 4.022e-05 2.928e-07
## beta3 4.992e-03 1.501e-04
## beta4 6.966e-04 1.466e-04
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 7.984e-07 
##   [2] Flicker
##        Estimated parameters : sigma2 = 1.006e-06 
## 
## Runtime (seconds)
##   Total              : 2.3383

Monte Carlo simulation 

B_fl = 100
mat_res_fl = matrix(NA, nrow = B_fl, ncol = 18)
for(b in seq(B_fl)){
  eps = generate(wn(sigma2_wn_fl) + flicker(sigma2 = sigma2_fl),
                 n = n, seed = (123 + b))$series
  y = X %*% beta + eps
  fit = gmwmx2(X = X, y = y, model = wn() + flicker())
  fit2 = lm(y~X[,2] + X[,3] + X[,4])

  mat_res_fl[b, ] = c(fit$beta_hat, fit$std_beta_hat,
                      summary(fit2)$coefficients[,1],
                      summary(fit2)$coefficients[,2],
                      fit$theta_domain$`Flicker_2`,
                      fit$theta_domain$`White Noise_1`)
  # cat("Iteration ", b, " \n")
}

mat_res_fl_df = as.data.frame(mat_res_fl)
colnames(mat_res_fl_df) = c("gmwmx_beta0_hat", "gmwmx_beta1_hat",
                            "gmwmx_beta2_hat", "gmwmx_beta3_hat",
                            "gmwmx_std_beta0_hat", "gmwmx_std_beta1_hat",
                            "gmwmx_std_beta2_hat", "gmwmx_std_beta3_hat",
                            "lm_beta0_hat", "lm_beta1_hat", "lm_beta2_hat", "lm_beta3_hat",
                            "lm_std_beta0_hat", "lm_std_beta1_hat",
                            "lm_std_beta2_hat", "lm_std_beta3_hat",
                            "sigma2_fl" ,"sigma2_wn")

Plot empirical distributions of estimated parameters 

par(mfrow = c(1, 4))
boxplot_mean_dot(mat_res_df[, c("gmwmx_beta0_hat")],las=1,
        names = c("beta0"),
        main = expression(beta[0]), ylab = "Estimate")
abline(h = beta[1], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta1_hat")],las=1,
        names = c("beta1"),
        main = expression(beta[1]), ylab = "Estimate")
abline(h = beta[2], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta2_hat")],las=1,
        names = c("beta2"),
        main = expression(beta[2]), ylab = "Estimate")
abline(h = beta[3], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta3_hat")],las=1,
        names = c("beta3"),
        main = expression(beta[3]), ylab = "Estimate")
abline(h = beta[4], col = "black", lwd = 2)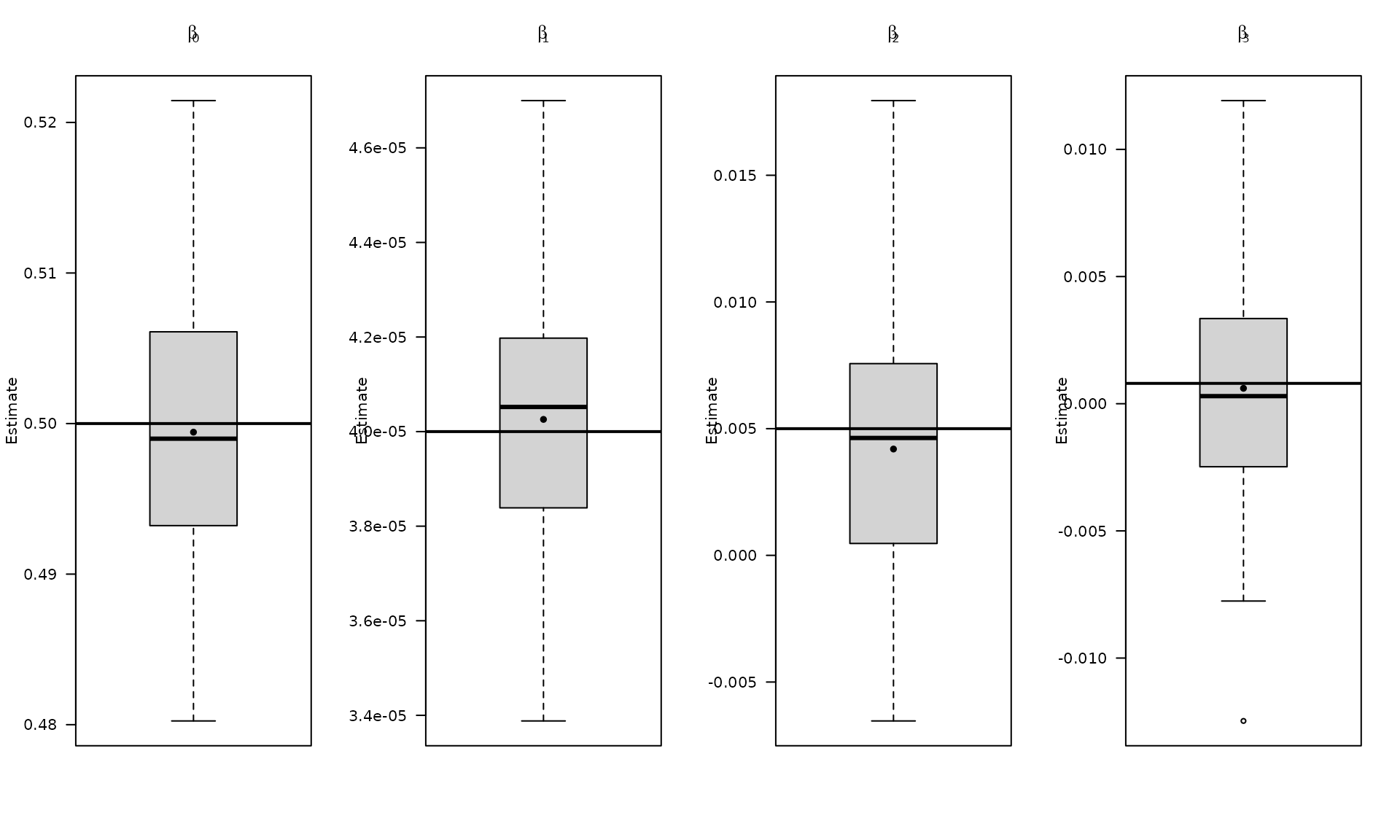

par(mfrow = c(1, 1))
par(mfrow = c(1, 2))

boxplot_mean_dot(mat_res_fl_df$sigma2_fl,las=1,
        main = expression(sigma["FL"]^2), ylab = "Estimate")
abline(h = sigma2_fl, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_fl_df$sigma2_wn,las=1,
        names = c("phi_ar1"),
        main = expression(sigma["WN"]^2), ylab = "Estimate")
abline(h = sigma2_wn_fl, col = "black", lwd = 2)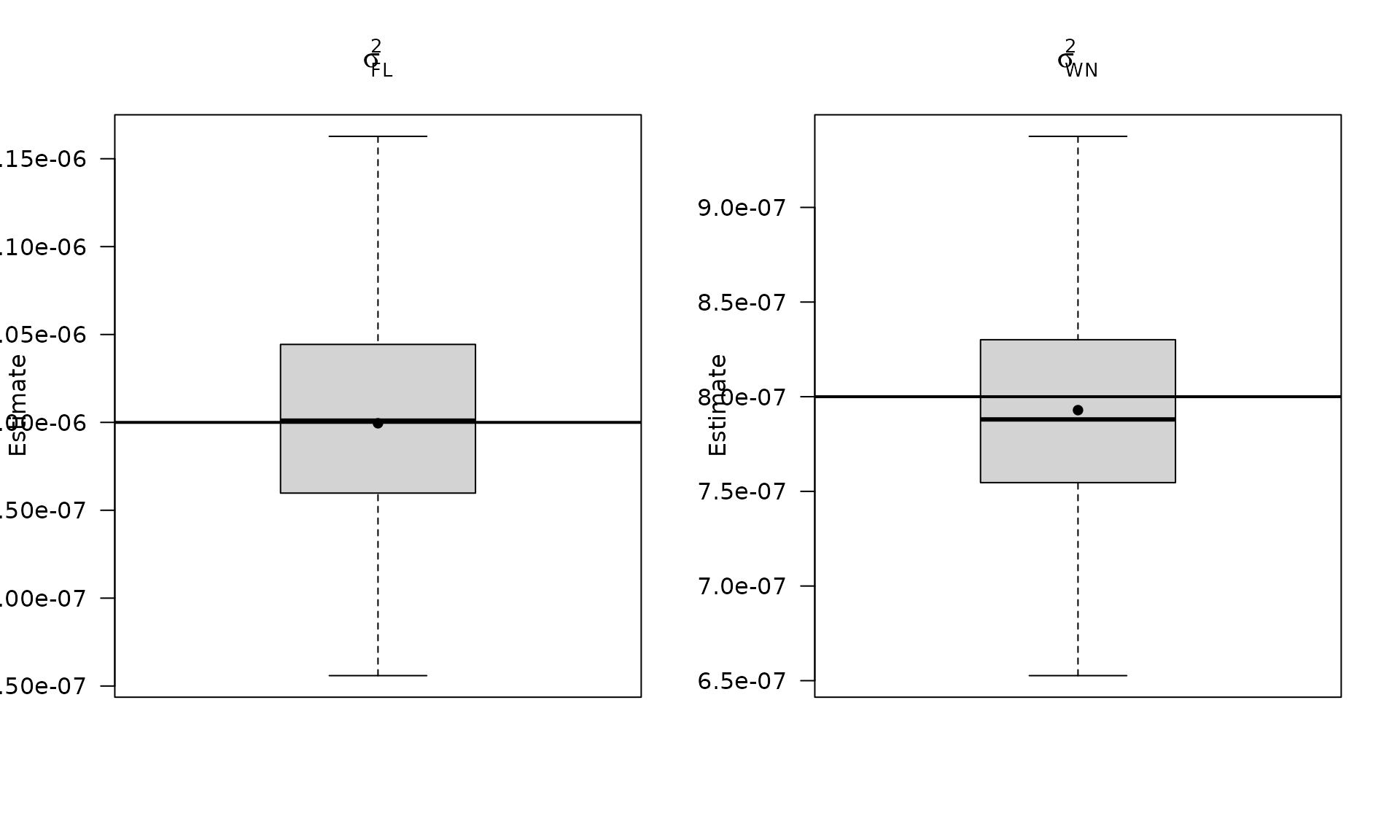

par(mfrow = c(1, 1))

Compute empirical coverage of confidence intervals 

zval = qnorm(0.975)
mat_res_fl_df$upper_ci_gmwmx_beta1 = mat_res_fl_df$gmwmx_beta1_hat + zval * mat_res_fl_df$gmwmx_std_beta1_hat
mat_res_fl_df$lower_ci_gmwmx_beta1 = mat_res_fl_df$gmwmx_beta1_hat - zval * mat_res_fl_df$gmwmx_std_beta1_hat
# empirical coverage of gmwmx beta
dplyr::between(rep(beta[2], B_pl), mat_res_fl_df$lower_ci_gmwmx_beta1, mat_res_fl_df$upper_ci_gmwmx_beta1) %>% mean()
## [1] 0.94
# do the same for lm beta
mat_res_fl_df$upper_ci_lm_beta1 = mat_res_fl_df$lm_beta1_hat + zval * mat_res_fl_df$lm_std_beta1_hat
mat_res_fl_df$lower_ci_lm_beta1 = mat_res_fl_df$lm_beta1_hat - zval * mat_res_fl_df$lm_std_beta1_hat
dplyr::between(rep(beta[2], B_pl), mat_res_fl_df$lower_ci_lm_beta1, mat_res_fl_df$upper_ci_lm_beta1) %>% mean()
## [1] 0.07
Guerrier, StΓ©phane, Jan Skaloud, Yannick Stebler, and Maria-Pia Victoria-Feser. 2013. β€œWavelet-Variance-based Estimation for Composite Stochastic Processes.” Journal of the American Statistical Association 108 (503): 1021–30.
Xu, Haotian, StΓ©phane Guerrier, Roberto Molinari, and Yuming Zhang. 2017. β€œA Study of the Allan Variance for Constant-mean Nonstationary Processes.” IEEE Signal Processing Letters 24 (8): 1257–60.
Zhang, Nien Fan. 2008. β€œAllan Variance of Time Series Models for Measurement Data.” Metrologia 45 (5): 549.