GMWMX: Estimate linear models with dependent errors and missing observations • gmwmx2

This vignette demonstrates how to use the GMWMX estimator to estimate linear models with dependent errors described by a composite stochastic process in the presence of missing observations. Consider the model defined as:

$\begin{equation} \mathbf{Y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}, \quad \boldsymbol{\varepsilon} \sim \mathcal{F}\left\{\mathbf{0}, \boldsymbol{\Sigma}\left(\boldsymbol{\gamma}\right)\right\}, \end{equation}$

where $\mathbf{X} \in \mathbb{R}^{n \times p}$ is a design matrix of observed predictors, $\boldsymbol{\beta} \in \mathbb{R}^p$ is the regression parameter vector and $\boldsymbol{\varepsilon} = \{\varepsilon_{i}\}_{i=1,\ldots,n}$ is a zero-mean process following an unspecified joint distribution $\mathcal{F}$ with positive-definite covariance function $\boldsymbol{\Sigma}(\boldsymbol{\gamma}) \in \mathbb{R}^{n\times n}$ characterizing the second-order dependence structure of the process and parameterized by the vector $\boldsymbol{\gamma} \in \boldsymbol{\Gamma} \subset \mathbb{R}^q$ .

Missingness is modeled by a binary process $\mathbf{Z} \in \{0,1\}^n$ with $Z_i = 1$ indicating an observation and $Z_i = 0$ a missing observation. The missingness process is independent of $\mathbf{Y}$ and assumes the definition:

$\begin{equation} Z_i = \begin{cases} Z_{i-1}, & \text{with probability } \rho, \\ W_i \sim \mathrm{Bernoulli}(\mu(\bm{\vartheta})), & \text{with probability } 1-\rho, \end{cases} \end{equation}$

with expectation $\mu(\boldsymbol{\vartheta}) = \mathbb{E}[Z_i] \in (0, 1]$ for all $i \in \{1, \ldots, n\}$ , with covariance matrix $\boldsymbol{\Lambda}(\boldsymbol{\vartheta}) = \operatorname{var}\left(\mathbf{Z}\right) \in \mathbb{R}^{n\times n}$ whose structure is assumed known up to the parameter vector $\boldsymbol{\vartheta} \in \boldsymbol{\Upsilon} \subset \mathbb{R}^k$ . The observed series is

$\tilde{\mathbf{Y}} = \mathbf{Y} \odot \mathbf{Z}.$

The design matrix with rows zeroed out for missing observations can be written as $\tilde{\mathbf{X}} = \left(\mathbf{Z} \otimes \mathbf{1}^T\right) \odot \mathbf{X}$ . The least‑squares estimator based on observed data is

$\hat{\boldsymbol{\beta}} = \left(\tilde{\mathbf{X}}^T \tilde{\mathbf{X}}\right)^{-1}\tilde{\mathbf{X}}^T \tilde{\mathbf{Y}},$

and we compute residuals

$\begin{equation} \hat{\boldsymbol{\varepsilon}} = \tilde{\mathbf{Y}} - \tilde{\mathbf{X}}\hat{\boldsymbol{\beta}}. \end{equation}$

We then obtain $\hat{\boldsymbol{\vartheta}}$ , the estimated parameters of the missingness process using the maximum likelihood estimator, assuming a two-state Markov model.

We then estimate the stochastic parameters using the GMWM estimator:

$\begin{equation} \hat{\boldsymbol{\gamma}} = \underset{\boldsymbol{\gamma} \in \boldsymbol{\Gamma}}{\arg\min} \,\left\{\hat{\boldsymbol{\nu}} - \boldsymbol{\nu}(\boldsymbol{\gamma}, \hat{\boldsymbol{\vartheta}})\right\}^{T} \, \boldsymbol{\Omega} \, \left\{\hat{\boldsymbol{\nu}} - \boldsymbol{\nu}(\boldsymbol{\gamma}, \hat{\boldsymbol{\vartheta}})\right\}, \end{equation}$

where $\hat{\boldsymbol{\nu}}$ is the estimated wavelet variance computed on the estimated residuals $\hat{\boldsymbol{\varepsilon}}$ and $\hat{\boldsymbol{\vartheta}}$ is the pre-computed estimator of the parameter $\boldsymbol{\vartheta}$ , with $\boldsymbol{\Omega}$ being any positive-definite matrix.

The variance-covariance matrix of the estimated regression parameters $\hat{\boldsymbol{\beta}}$ is then obtained as:

$\begin{equation} \mu(\hat{\boldsymbol{\vartheta}})^{-2}(\mathbf{X}^{\top}\mathbf{X})^{-1} \mathbf{X}^{\top} \boldsymbol{\Sigma}(\hat{\boldsymbol{\gamma}}, \hat{\boldsymbol{\vartheta}}) \mathbf{X} (\mathbf{X}^{\top}\mathbf{X})^{-1}. \end{equation}$

where $\boldsymbol{\Sigma}(\hat{\boldsymbol{\gamma}}, \hat{\boldsymbol{\vartheta}}) = \left\{\boldsymbol{\Lambda}(\hat{\boldsymbol{\vartheta}}) + \mu(\hat{\boldsymbol{\vartheta}})^2 \mathbf{1}\mathbf{1}^{\top}\right\} \odot \boldsymbol{\Sigma}(\hat{\boldsymbol{\gamma}})$ .

Overall, these examples illustrate how gmwmx2() supports inference for linear regression models with dependent errors in presence of missing observations, and how the results compare to a naive OLS fit that ignores dependence.

We load the packages used for simulation, wavelet variance diagnostics, and summary plots. The helper boxplot_mean_dot() overlays Monte Carlo means on top of each boxplot for easier comparison.

library(gmwmx2)
library(wv)
library(dplyr)

boxplot_mean_dot <- function(x, ...) {
  boxplot(x, ...)
  x_mat <- as.matrix(x)
  mean_vals <- colMeans(x_mat, na.rm = TRUE)
  points(seq_along(mean_vals), mean_vals, pch = 16, col = "black")
}

We first construct a design matrix with an intercept, linear trend, and annual seasonal components. This deterministic signal will be used across examples.

Build an arbitrary design matrix X

n = 15*365
X = matrix(NA, nrow = n, ncol = 4)
# intercept
X[, 1] = 1
# trend
X[, 2] = 1:n
# annual sinusoid
omega_1 <- (1 / 365.25) * 2 * pi
X[, 3] <- sin((1:n) * omega_1)
X[, 4] <- cos((1:n) * omega_1)
beta = c(0.5 , 0.00004, 0.005,  0.0008)

# visualize the deterministic signal
plot(x = X[, 2], y = X %*% beta, type = "l",
     main = "Signal", xlab = "Time", ylab = "Signal")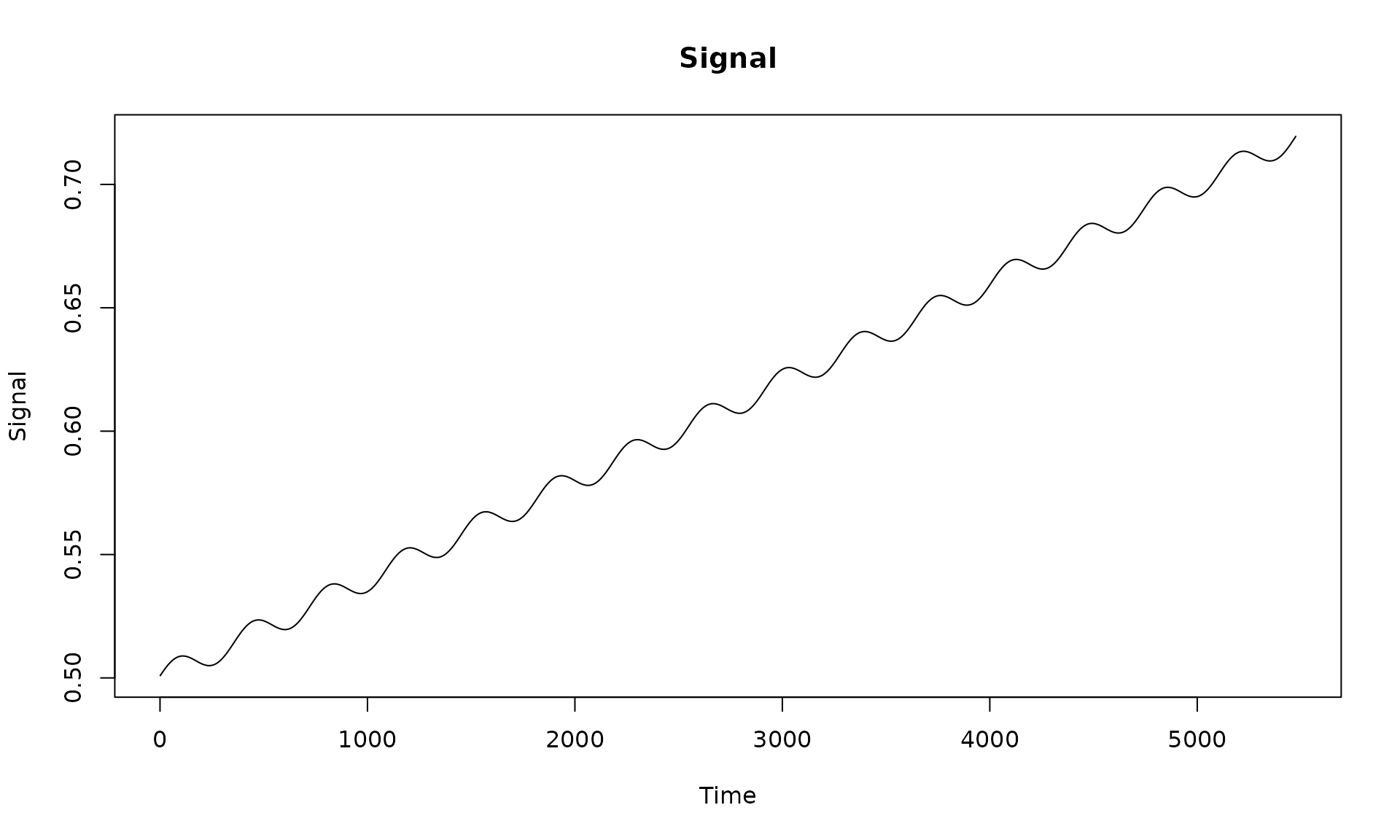

Next we simulate dependent errors, add them to the signal, and then introduce missing observations using a two‑state Markov model.

Example 1: White noise + AR(1)

Generate signal

phi_ar1 = 0.975
sigma2_ar1 =  5e-05
sigma2_wn =  7e-04
eps = generate(ar1(phi = phi_ar1, sigma2 = sigma2_ar1) + wn(sigma2_wn), n = n, seed = 123)$series
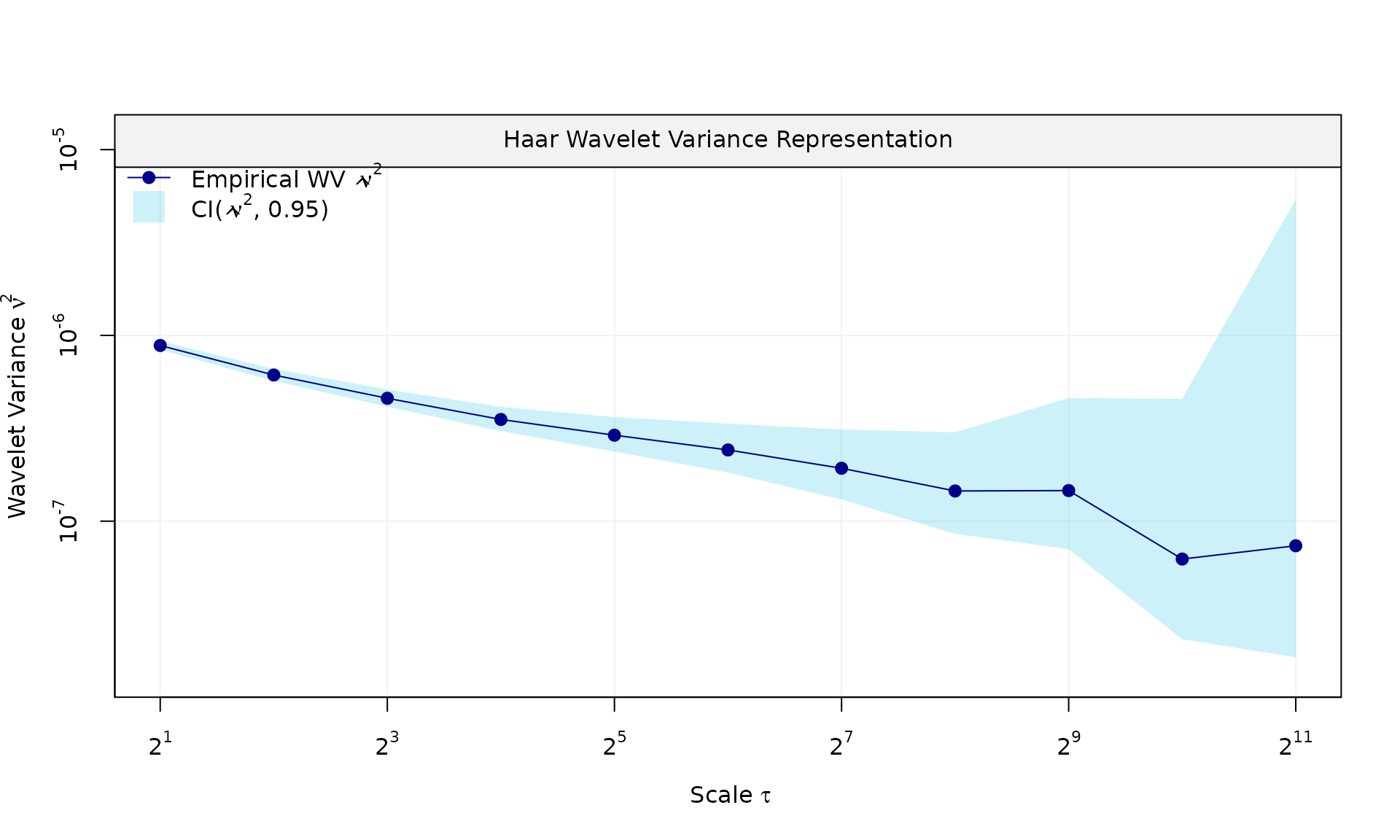
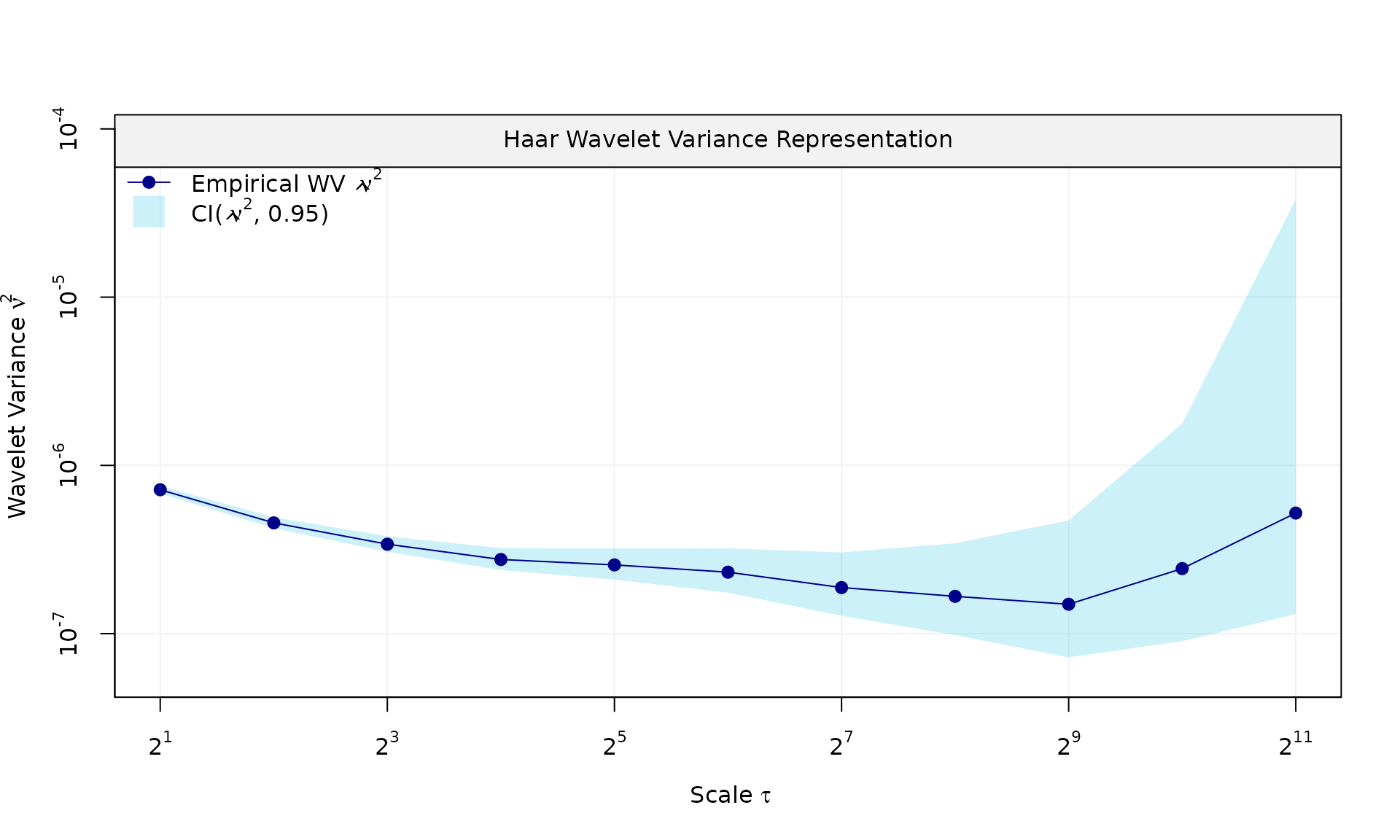
plot(wv::wvar(eps))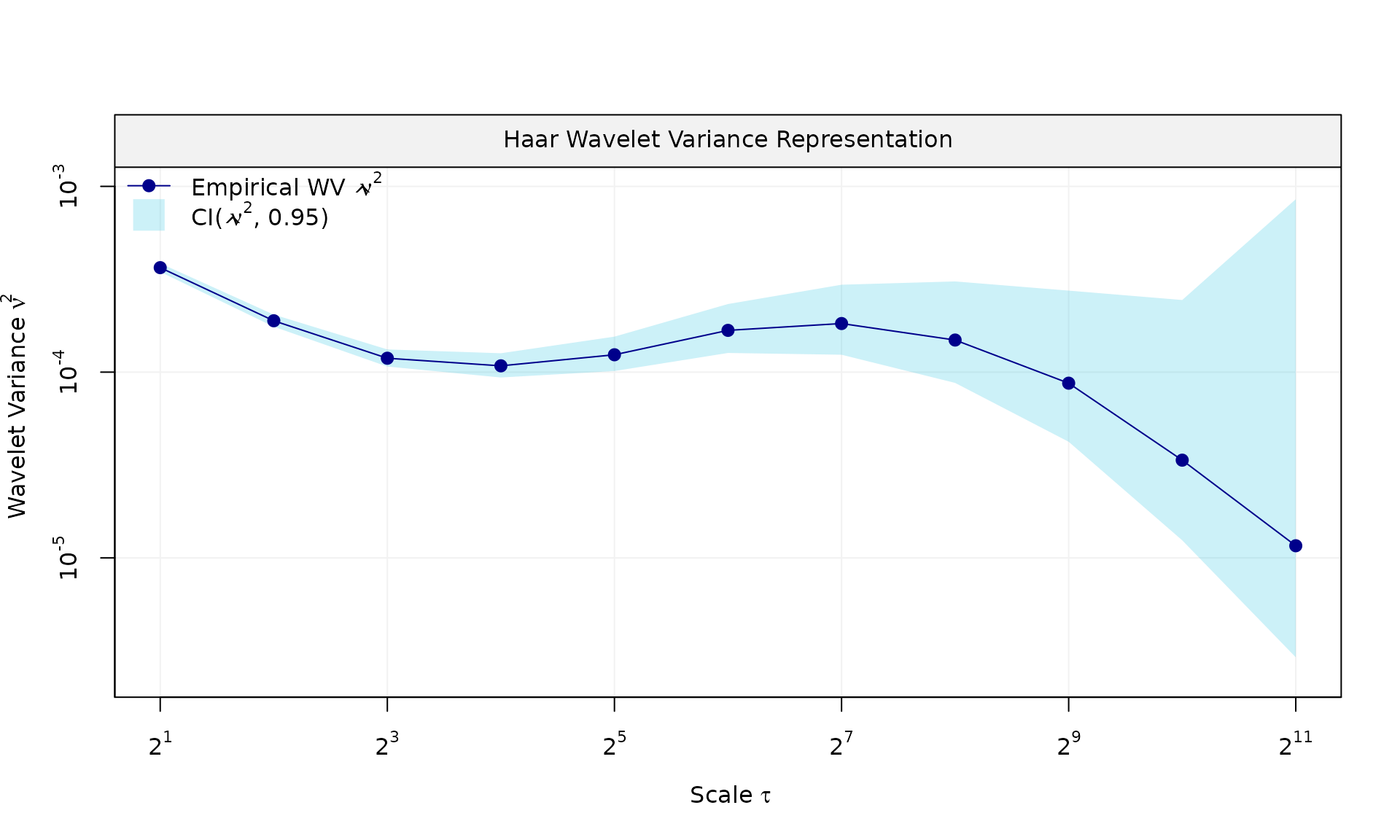

y = X %*% beta + eps

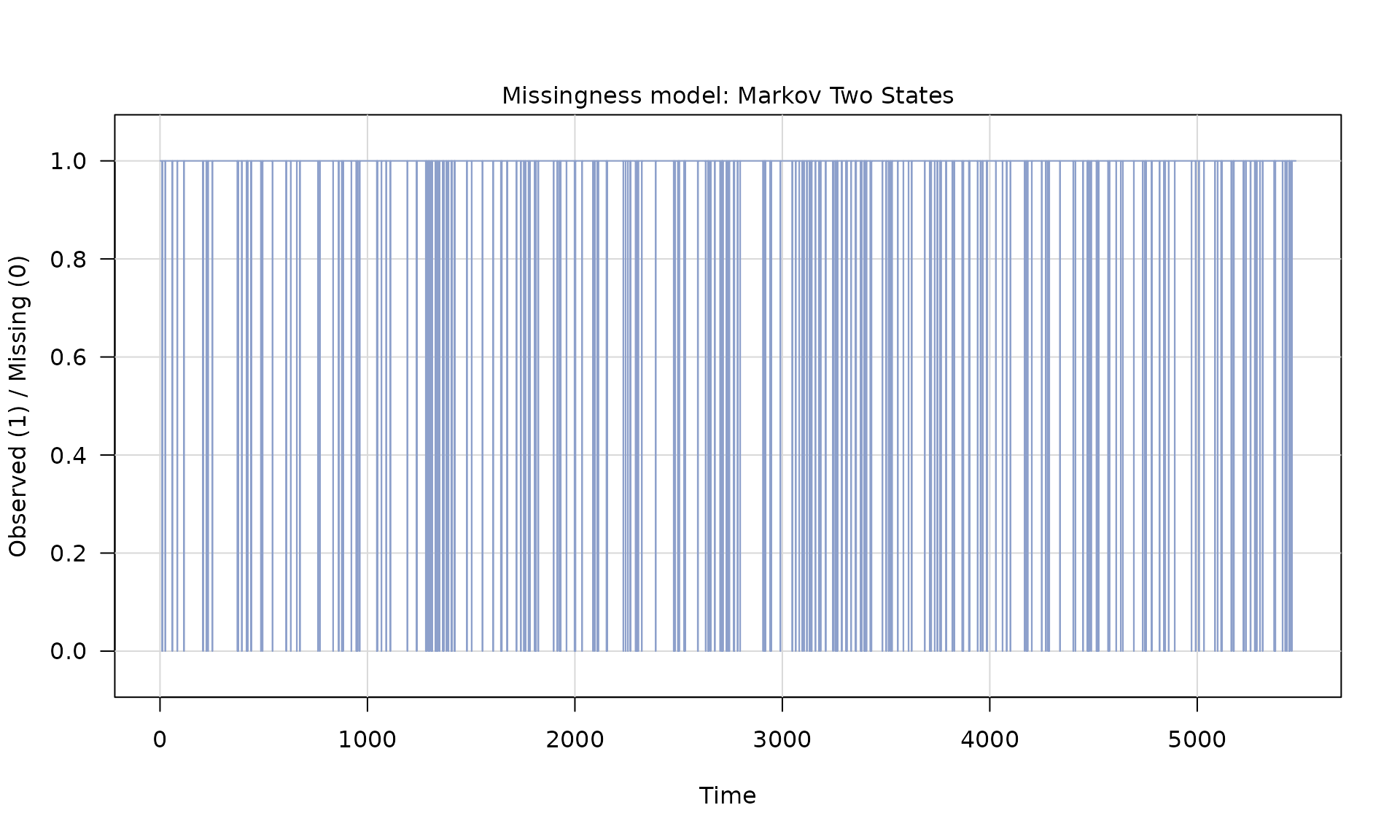
# generate missingness
mod_missing = markov_two_states(p1 = 0.05, p2 = .95)
Z = generate(mod_missing, n = n, seed = 123)
plot(Z)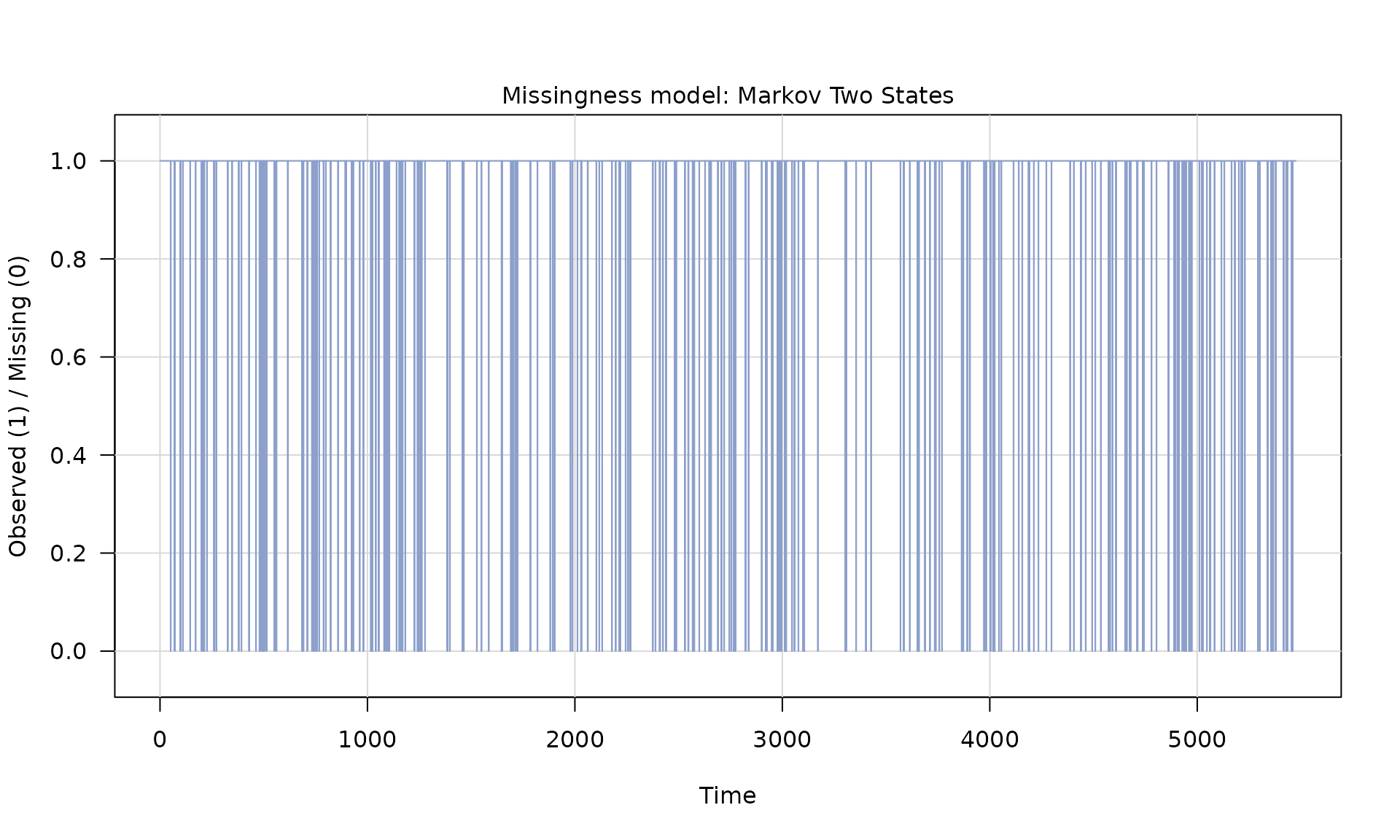

Z_process = Z$series
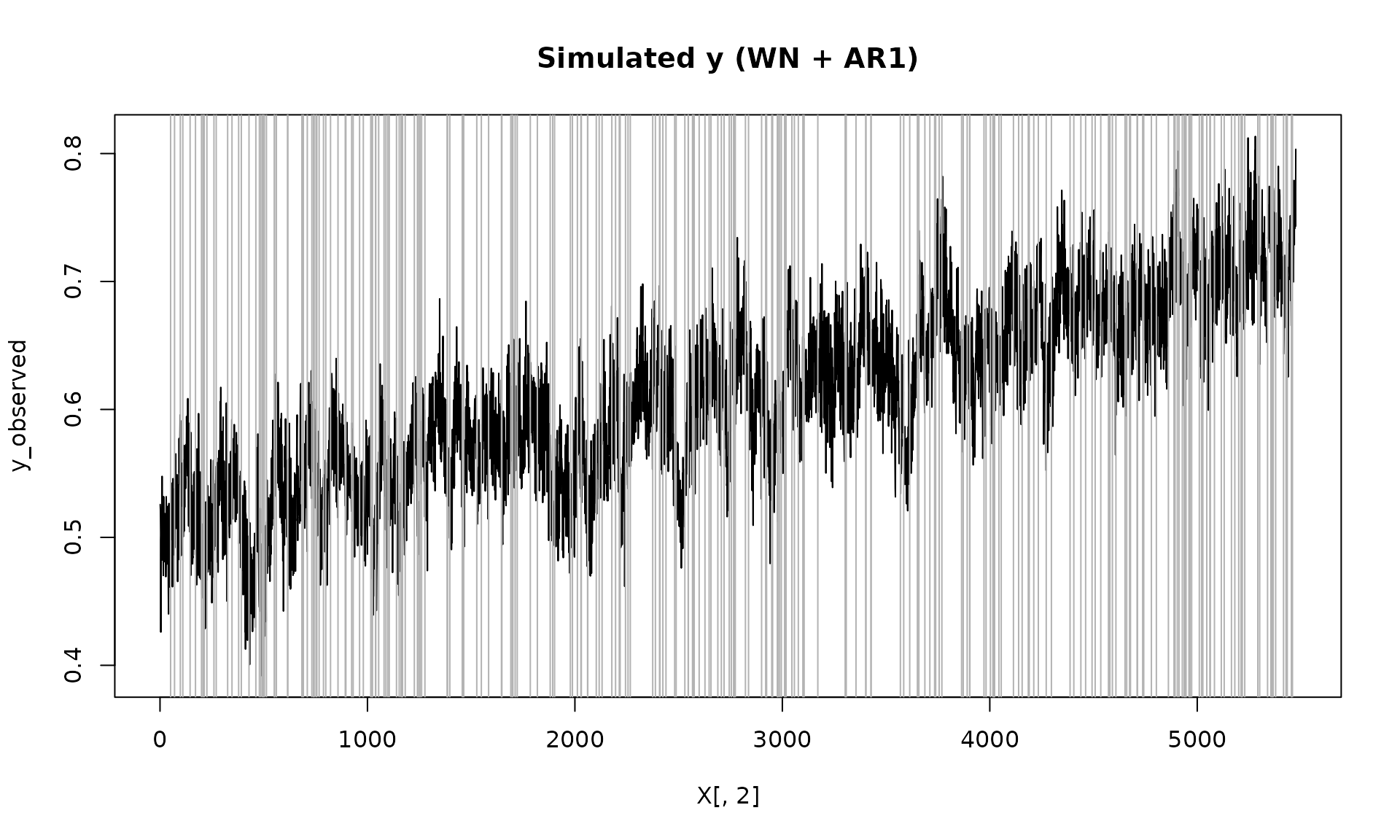
y_observed = ifelse(Z_process == 1, y, NA)
plot(X[, 2], y_observed, type = "l", main = "Simulated y (WN + AR1)")



id_not_observed = which(is.na(y_observed))
for(i in id_not_observed){
  abline(v = X[i, 2], col = "grey70", lty =1)
}

We then fit the dependent‑error regression using gmwmx2(), which accounts for the stochastic error model and the missing observations.

Fit model

fit = gmwmx2(X = X, y = y_observed, model = wn() + ar1() )
print(fit)

## GMWMX fit
##         Estimate Std.Error
## beta1  5.061e-01 6.507e-03
## beta2  3.797e-05 2.056e-06
## beta3  5.107e-03 4.057e-03
## beta4 -4.780e-03 4.031e-03
## 
## Missingness model
##   Proportion missing : 0.0482 
##   p1                 : 0.0480 
##   p2                 : 0.9470 
##   p*                 : 0.9518 
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 0.0006826 
##   [2] AR(1)
##        Estimated parameters : phi = 0.9698, sigma2 = 5.296e-05 
## 
## Runtime (seconds)
##   Total              : 2.5394

Monte Carlo simulation

We now assess inference quality under missingness by repeating the simulation, fitting the correct dependent‑error model with gmwmx2(), and comparing against a misspecified OLS fit that treats the errors as i.i.d. and uses only observed data.

B = 100
mat_res = matrix(NA, nrow=B, ncol=19)
for(b in seq(B)){

  eps = generate(ar1(phi=phi_ar1, sigma2=sigma2_ar1) + wn(sigma2_wn), n=n, seed = (123 + b))$series
  y = X %*% beta + eps
  Z = generate(mod_missing, n = n, seed = 123 + b)$series
  y_observed = ifelse(Z == 1, y, NA)
  fit = gmwmx2(X = X, y = y_observed, model = wn() + ar1() )
  # misspecified model assuming white noise as the stochastic model and only on observed data
  fit2 = lm(y_observed~X[,2] + X[,3] + X[,4])

  mat_res[b, ] = c(fit$beta_hat, fit$std_beta_hat,
                   summary(fit2)$coefficients[,1],
                   summary(fit2)$coefficients[,2],
                   fit$theta_domain$`AR(1)_2`,
                   fit$theta_domain$`White Noise_1`)
  # cat("Iteration ", b, " completed.\n")
}

Plot empirical distributions of estimated parameters

# compute empirical coverage
mat_res_df = as.data.frame(mat_res)
colnames(mat_res_df) = c("gmwmx_beta0_hat", "gmwmx_beta1_hat",
                         "gmwmx_beta2_hat", "gmwmx_beta3_hat",
                         "gmwmx_std_beta0_hat", "gmwmx_std_beta1_hat",
                         "gmwmx_std_beta2_hat", "gmwmx_std_beta3_hat",
                         "lm_beta0_hat", "lm_beta1_hat", "lm_beta2_hat", "lm_beta3_hat",
                         "lm_std_beta0_hat", "lm_std_beta1_hat", "lm_std_beta2_hat", "lm_std_beta3_hat",
                         "phi_ar1","sigma_2_ar1" ,"sigma_2_wn")



par(mfrow = c(1, 4))
boxplot_mean_dot(mat_res_df[, c("gmwmx_beta0_hat")],las=1,
                 names = c("beta0"),
                 main = expression(beta[0]), ylab = "Estimate")
abline(h = beta[1], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta1_hat")],las=1,
                 names = c("beta1"),
                 main = expression(beta[1]), ylab = "Estimate")
abline(h = beta[2], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta2_hat")],las=1,
                 names = c("beta2"),
                 main = expression(beta[2]), ylab = "Estimate")
abline(h = beta[3], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta3_hat")],las=1,
                 names = c("beta3"),
                 main = expression(beta[3]), ylab = "Estimate")
abline(h = beta[4], col = "black", lwd = 2)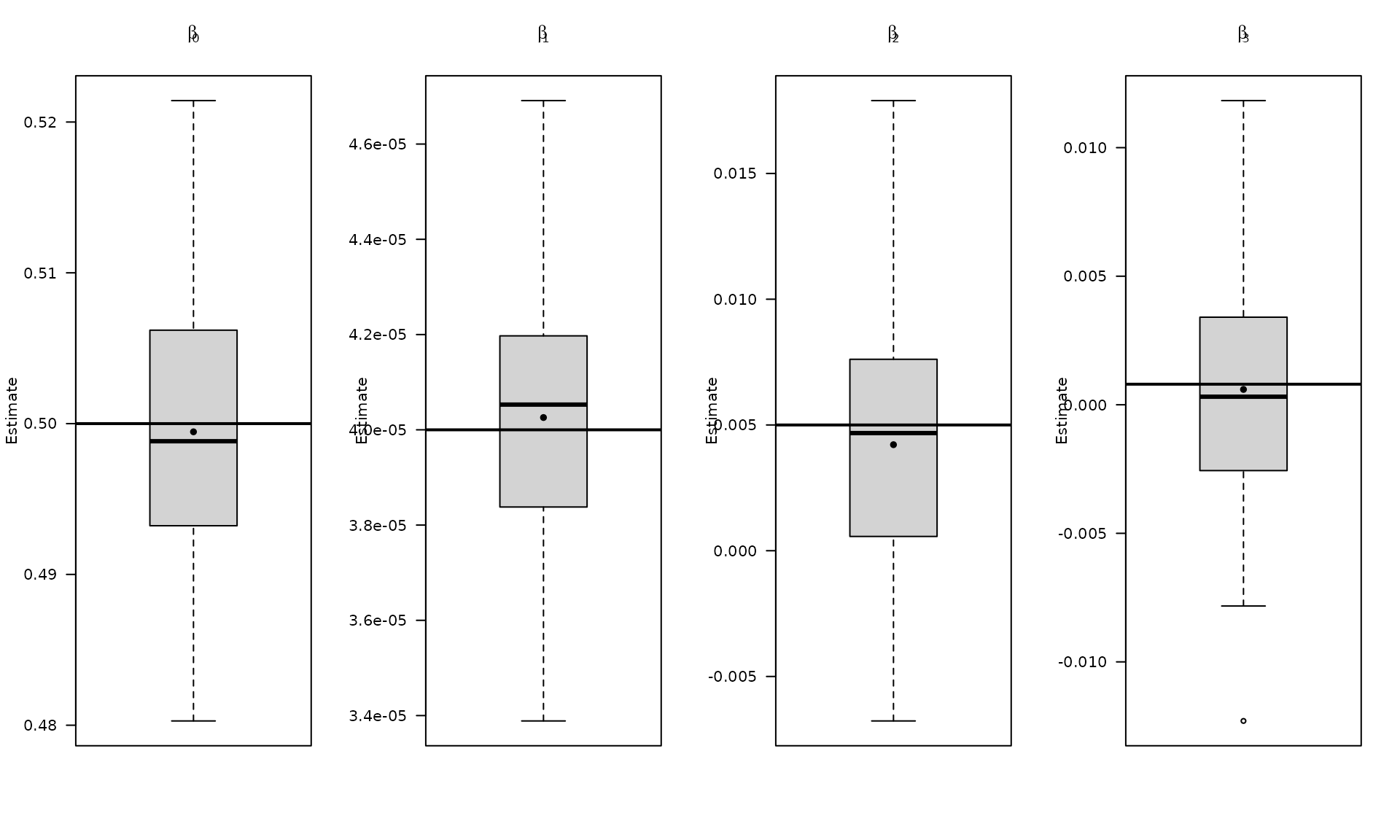

par(mfrow = c(1, 3))

boxplot_mean_dot(mat_res_df$phi_ar1,las=1,
                 names = c("phi_ar1"),
                 main = expression(phi["AR1"]), ylab = "Estimate")
abline(h = phi_ar1, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df$sigma_2_ar1,las=1,
                 names = c("phi_ar1"),
                 main = expression(sigma["AR1"]^2), ylab = "Estimate")
abline(h = sigma2_ar1, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df$sigma_2_wn,las=1,
                 names = c("phi_ar1"),
                 main = expression(sigma["WN"]^2), ylab = "Estimate")
abline(h = sigma2_wn, col = "black", lwd = 2)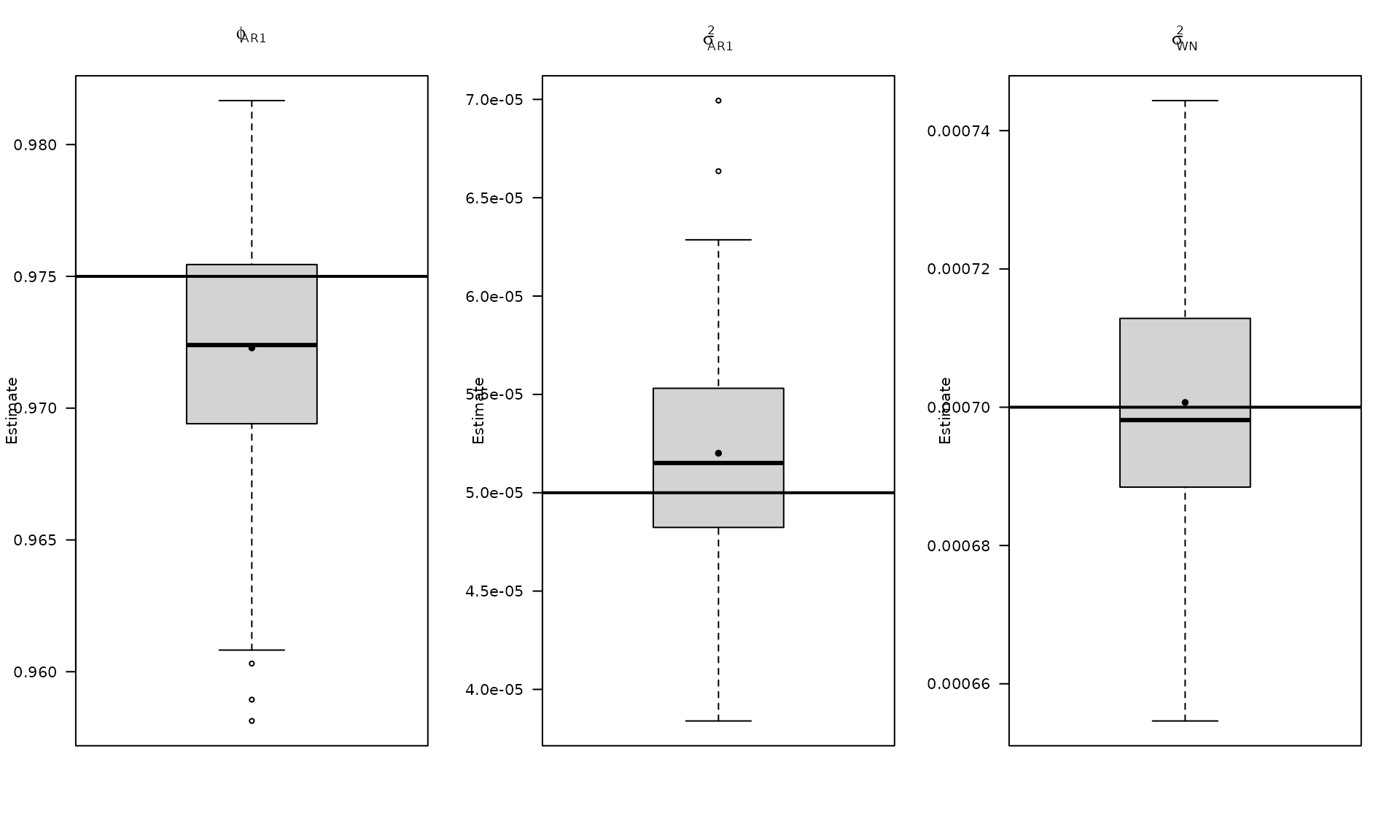

par(mfrow = c(1, 1))

The boxplots summarize the empirical distribution of the regression estimates and stochastic parameters across Monte Carlo replications, with the true values shown as horizontal lines.

We report the empirical fraction of times the true $\boldsymbol{\beta}$ entries fall inside the estimated intervals for both gmwmx2() and OLS.

Compute empirical coverage of confidence intervals

# Compute empirical coverage of confidence intervals for beta
zval = qnorm(0.975)
mat_res_df$upper_ci_gmwmx_beta1 = mat_res_df$gmwmx_beta1_hat + zval * mat_res_df$gmwmx_std_beta1_hat
mat_res_df$lower_ci_gmwmx_beta1 = mat_res_df$gmwmx_beta1_hat - zval * mat_res_df$gmwmx_std_beta1_hat
# empirical coverage of gmwmx beta
dplyr::between(rep(beta[2], B), mat_res_df$lower_ci_gmwmx_beta1, mat_res_df$upper_ci_gmwmx_beta1) %>% mean()

## [1] 0.88

# do the same for lm beta
mat_res_df$upper_ci_lm_beta1 = mat_res_df$lm_beta1_hat + zval * mat_res_df$lm_std_beta1_hat
mat_res_df$lower_ci_lm_beta1 = mat_res_df$lm_beta1_hat - zval * mat_res_df$lm_std_beta1_hat
dplyr::between(rep(beta[2], B), mat_res_df$lower_ci_lm_beta1, mat_res_df$upper_ci_lm_beta1) %>% mean()

## [1] 0.17

We now repeat the workflow for a long‑memory error model (white noise + stationary power‑law). The steps mirror the AR(1) case: simulate with missingness, fit gmwmx2(), and compare to a misspecified OLS fit.

The parameter $\kappa$ controls the long‑memory behavior of the power‑law component.

Example 2: White noise + stationary power-law

Generate signal

kappa_pl <- -0.75
sigma2_wn <- 2e-07
sigma2_pl <- 2.25e-06
eps_pl = generate(wn(sigma2_wn) + pl(kappa = kappa_pl, sigma2 = sigma2_pl),
                  n = n, seed = 1234)
plot(eps_pl$series, type = "l")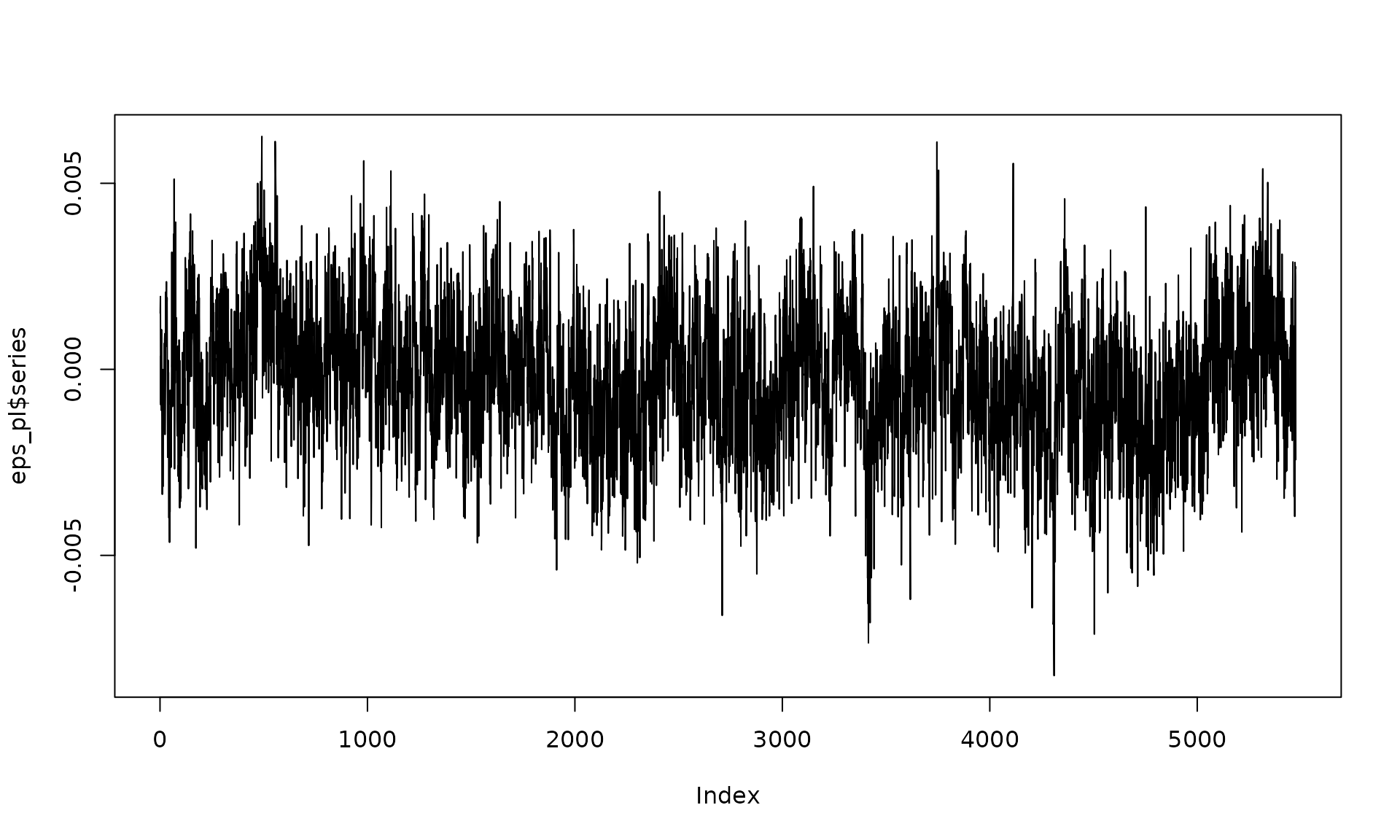

plot(wv::wvar(eps_pl$series))

y_pl = X %*% beta + eps_pl$series
Z = generate(mod_missing, n = n, seed = 1234)
plot(Z)

Z_process = Z$series
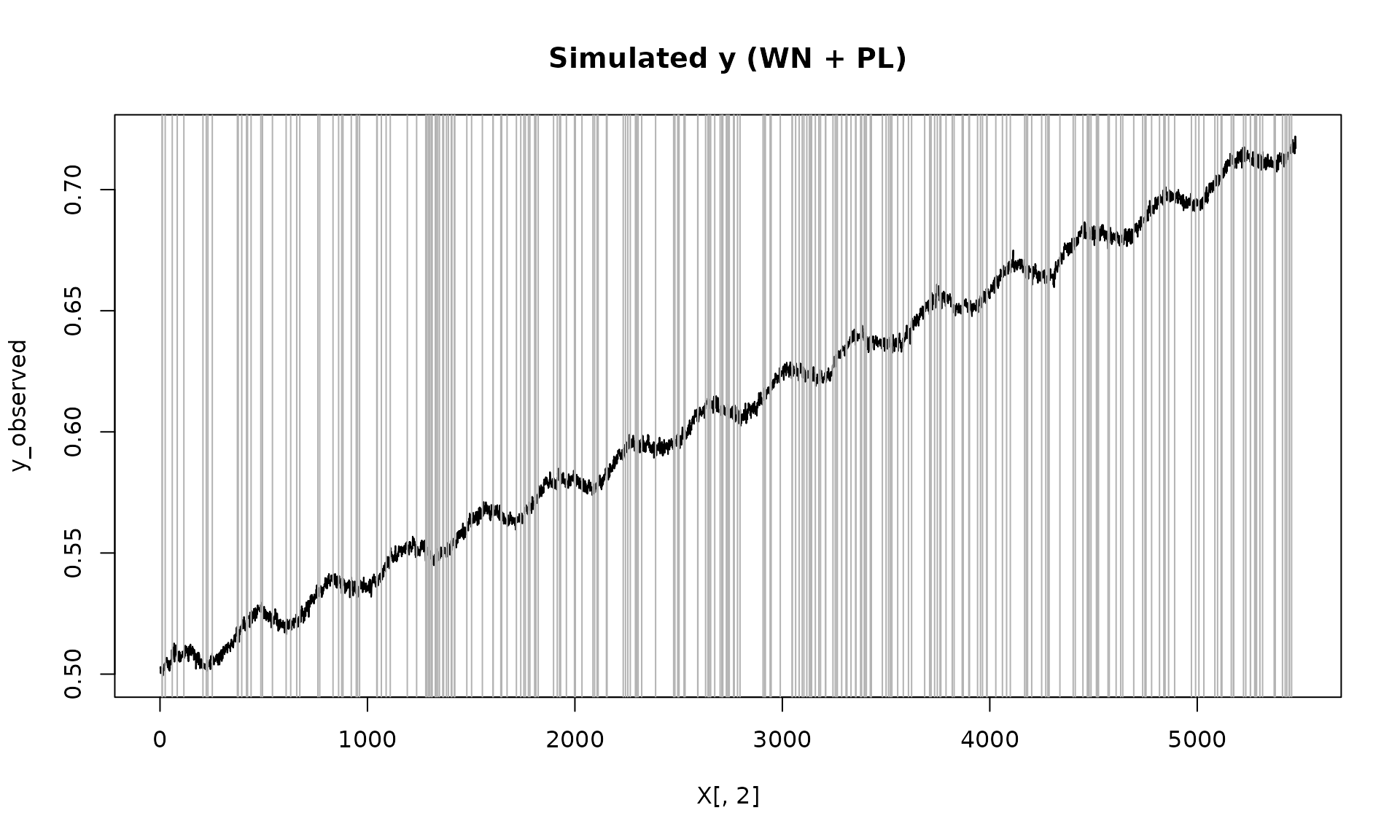
y_observed = ifelse(Z_process == 1, y_pl, NA)

plot(X[, 2], y_observed, type = "l", main = "Simulated y (WN + PL)")
id_not_observed = which(is.na(y_observed))
for(i in id_not_observed){
  abline(v = X[i, 2], col = "grey70", lty =1)
}

Fit model

fit_pl = gmwmx2(X = X, y = y_observed, model = wn() + pl())
fit_pl

## GMWMX fit
##        Estimate Std.Error
## beta1 5.002e-01 7.289e-04
## beta2 3.982e-05 1.702e-07
## beta3 4.977e-03 1.300e-04
## beta4 6.726e-04 1.281e-04
## 
## Missingness model
##   Proportion missing : 0.0482 
##   p1                 : 0.0482 
##   p2                 : 0.9508 
##   p*                 : 0.9518 
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 1.232e-14 
##   [2] Stationary PowerLaw
##        Estimated parameters : kappa = -0.7154, sigma2 = 2.46e-06 
## 
## Runtime (seconds)
##   Total              : 1.4071

Monte Carlo simulation

B_pl = 100
mat_res_pl = matrix(NA, nrow = B_pl, ncol = 19)
for(b in seq(B_pl)){
  eps = generate(wn(sigma2_wn) + pl(kappa = kappa_pl, sigma2 = sigma2_pl),
                 n = n, seed = (123 + b))$series
  y = X %*% beta + eps

  Z = generate(mod_missing, n = n, seed = (123 + b))
  Z_process = Z$series
  y_observed = ifelse(Z_process == 1, y, NA)

  fit = gmwmx2(X = X, y = y_observed, model = wn() + pl())
  fit2 = lm(y_observed~X[,2] + X[,3] + X[,4])

  mat_res_pl[b, ] = c(fit$beta_hat, fit$std_beta_hat,
                      summary(fit2)$coefficients[,1],
                      summary(fit2)$coefficients[,2],
                      fit$theta_domain$`Stationary PowerLaw_2`,
                      fit$theta_domain$`White Noise_1`)
  # cat("Iteration ", b, " \n")
}

Plot empirical distributions of estimated parameters

mat_res_pl_df = as.data.frame(mat_res_pl)
colnames(mat_res_pl_df) = c("gmwmx_beta0_hat", "gmwmx_beta1_hat",
                            "gmwmx_beta2_hat", "gmwmx_beta3_hat",
                            "gmwmx_std_beta0_hat", "gmwmx_std_beta1_hat",
                            "gmwmx_std_beta2_hat", "gmwmx_std_beta3_hat",
                            "lm_beta0_hat", "lm_beta1_hat", "lm_beta2_hat", "lm_beta3_hat",
                            "lm_std_beta0_hat", "lm_std_beta1_hat",
                            "lm_std_beta2_hat", "lm_std_beta3_hat",
                            "kappa_pl","sigma2_pl" ,"sigma2_wn")


# Plot empirical distributions (beta and stochastic parameters)


par(mfrow = c(1, 4))
boxplot_mean_dot(mat_res_df[, c("gmwmx_beta0_hat")],las=1,
                 names = c("beta0"),
                 main = expression(beta[0]), ylab = "Estimate")
abline(h = beta[1], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta1_hat")],las=1,
                 names = c("beta1"),
                 main = expression(beta[1]), ylab = "Estimate")
abline(h = beta[2], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta2_hat")],las=1,
                 names = c("beta2"),
                 main = expression(beta[2]), ylab = "Estimate")
abline(h = beta[3], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta3_hat")],las=1,
                 names = c("beta3"),
                 main = expression(beta[3]), ylab = "Estimate")
abline(h = beta[4], col = "black", lwd = 2)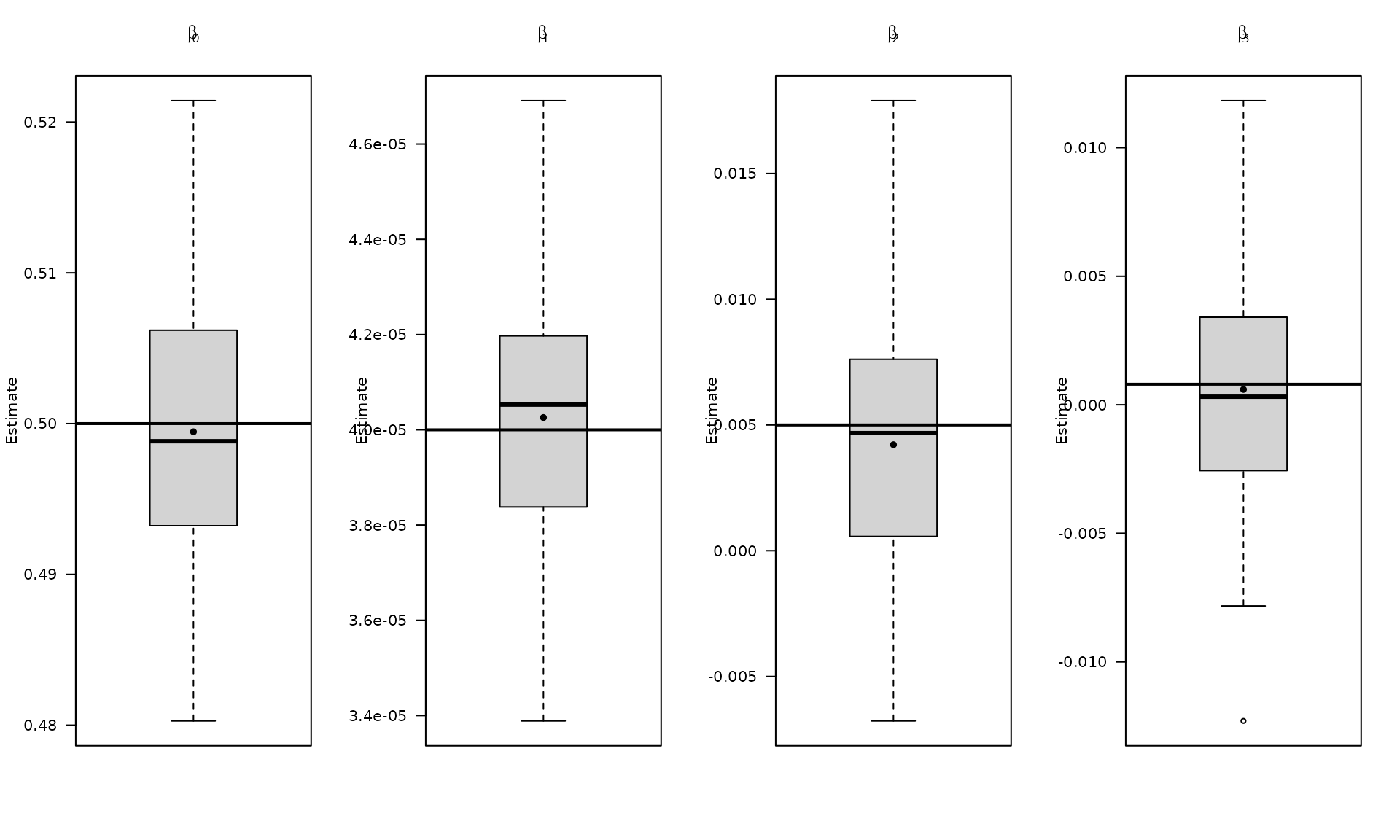

par(mfrow = c(1, 1))

par(mfrow = c(1, 3))

boxplot_mean_dot(mat_res_pl_df$kappa_pl,las=1,
                 main = expression(kappa["PL"]), ylab = "Estimate")
abline(h = kappa_pl, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_pl_df$sigma2_pl,las=1,
                 main = expression(sigma["PL"]^2), ylab = "Estimate")
abline(h = sigma2_pl, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_pl_df$sigma2_wn,las=1,
                 names = c("phi_ar1"),
                 main = expression(sigma["WN"]^2), ylab = "Estimate")
abline(h = sigma2_wn, col = "black", lwd = 2)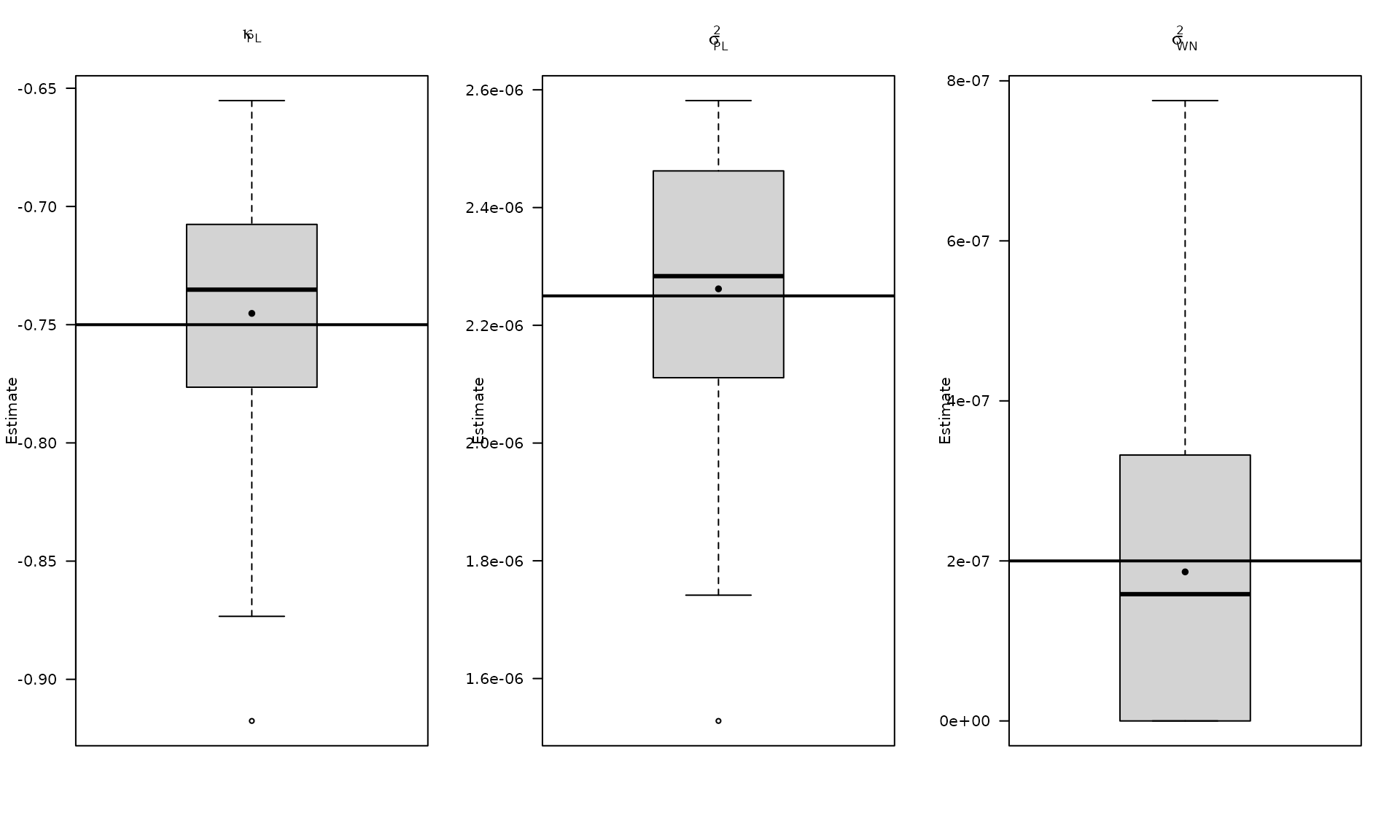

par(mfrow = c(1, 1))

Compute empirical coverage for the regression coefficients under the power‑law error model and compare against OLS.

Compute empirical coverage of confidence intervals

zval = qnorm(0.975)
mat_res_pl_df$upper_ci_gmwmx_beta1 = mat_res_pl_df$gmwmx_beta1_hat + zval * mat_res_pl_df$gmwmx_std_beta1_hat
mat_res_pl_df$lower_ci_gmwmx_beta1 = mat_res_pl_df$gmwmx_beta1_hat - zval * mat_res_pl_df$gmwmx_std_beta1_hat
# empirical coverage of gmwmx beta
dplyr::between(rep(beta[2], B_pl), mat_res_pl_df$lower_ci_gmwmx_beta1, mat_res_pl_df$upper_ci_gmwmx_beta1) %>% mean()

## [1] 0.92

# do the same for lm beta
mat_res_pl_df$upper_ci_lm_beta1 = mat_res_pl_df$lm_beta1_hat + zval * mat_res_pl_df$lm_std_beta1_hat
mat_res_pl_df$lower_ci_lm_beta1 = mat_res_pl_df$lm_beta1_hat - zval * mat_res_pl_df$lm_std_beta1_hat

dplyr::between(rep(beta[2], B_pl), mat_res_pl_df$lower_ci_lm_beta1, mat_res_pl_df$upper_ci_lm_beta1) %>% mean()

## [1] 0.2

Example 3: White noise + flicker

Generate signal

sigma2_wn_fl <- 8e-07
sigma2_fl <- 1e-06
eps_fl = generate(wn(sigma2_wn_fl) + flicker(sigma2 = sigma2_fl),
                  n = n, seed = 123)
plot(eps_fl$series, type = "l")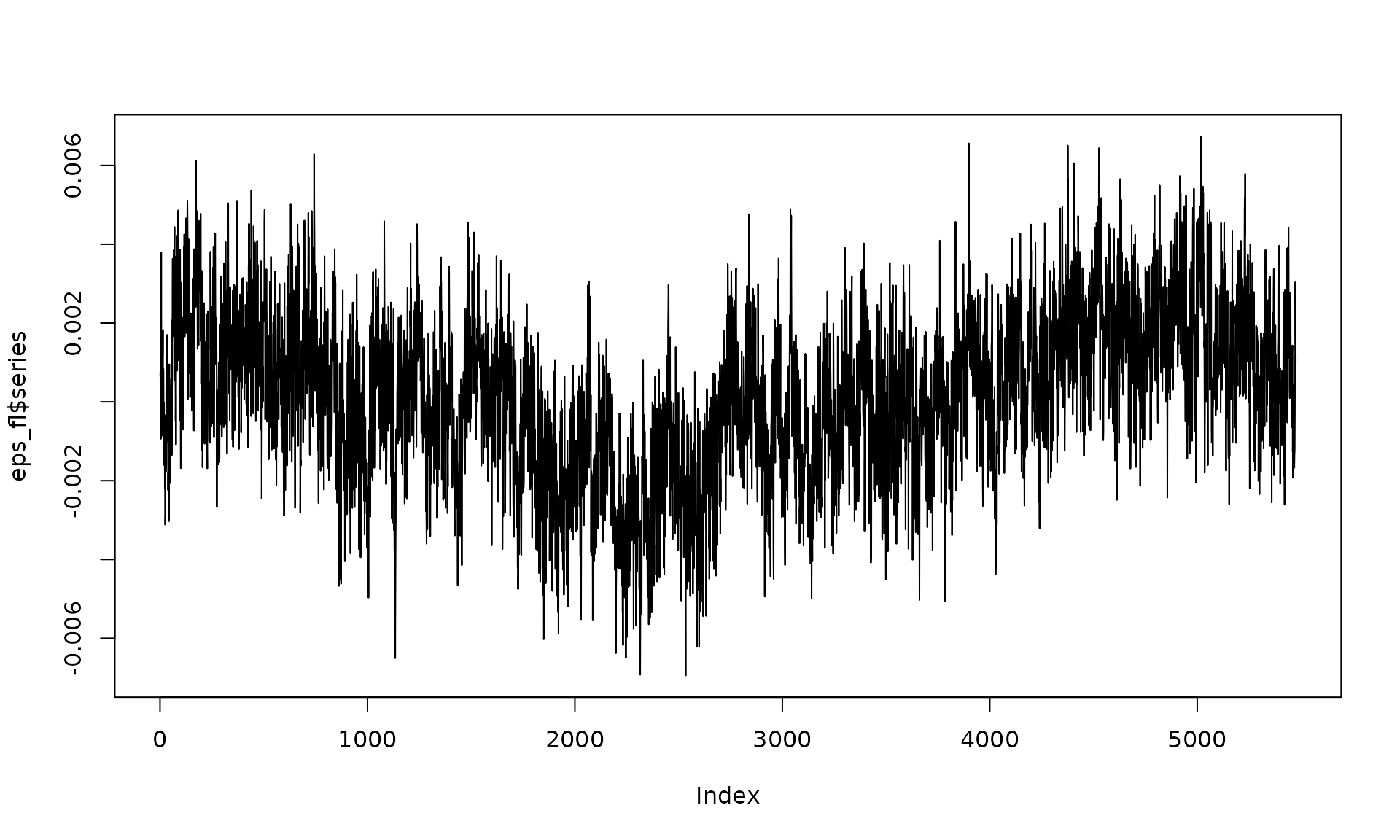

plot(wv::wvar(eps_fl$series))

Z = generate(mod_missing, n = n, seed = 1234)
plot(Z)

y_fl = X %*% beta + eps_fl$series

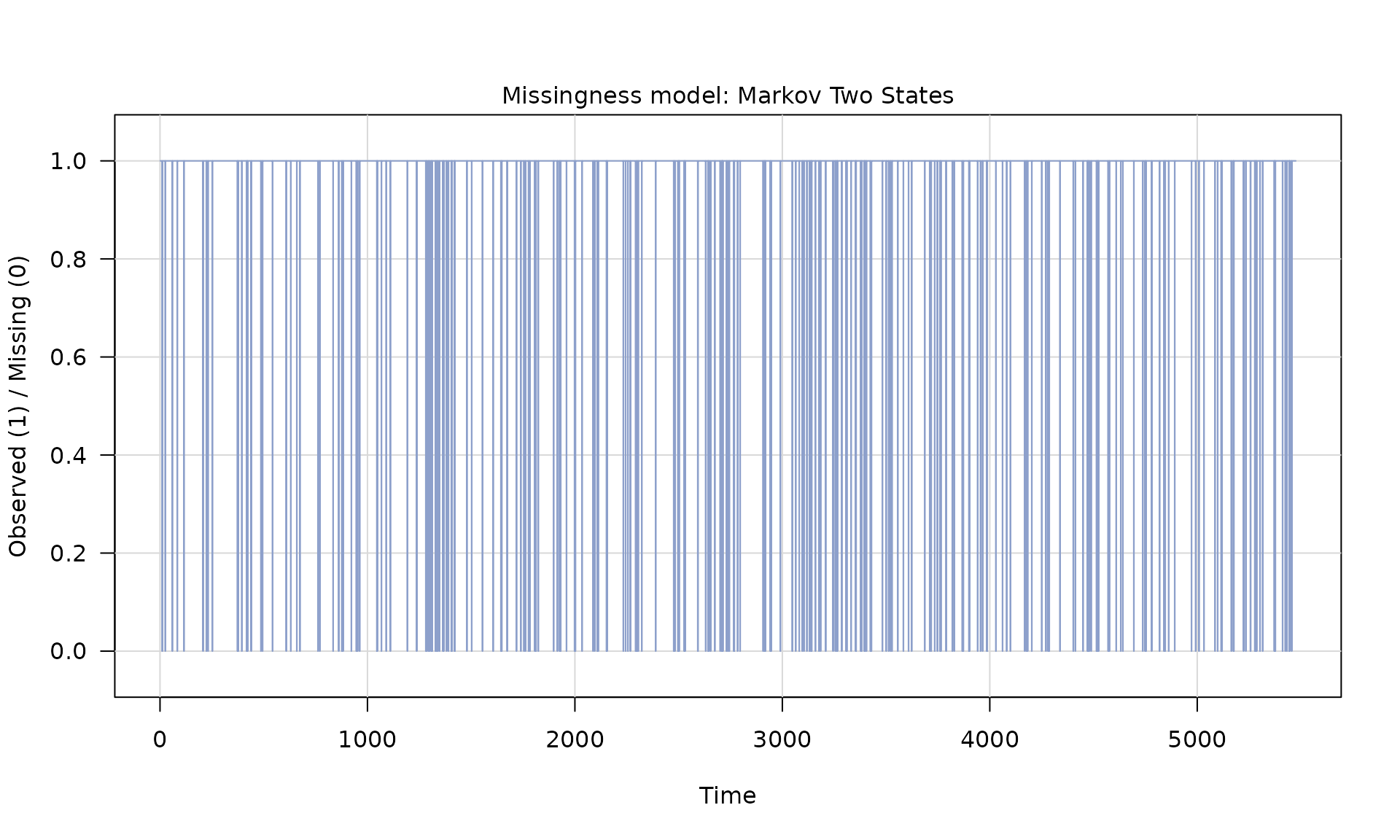
Z = generate(mod_missing, n = n, seed = 1234)
plot(Z)
Z_process = Z$series


y_observed = ifelse(Z_process == 1, y_fl, NA)

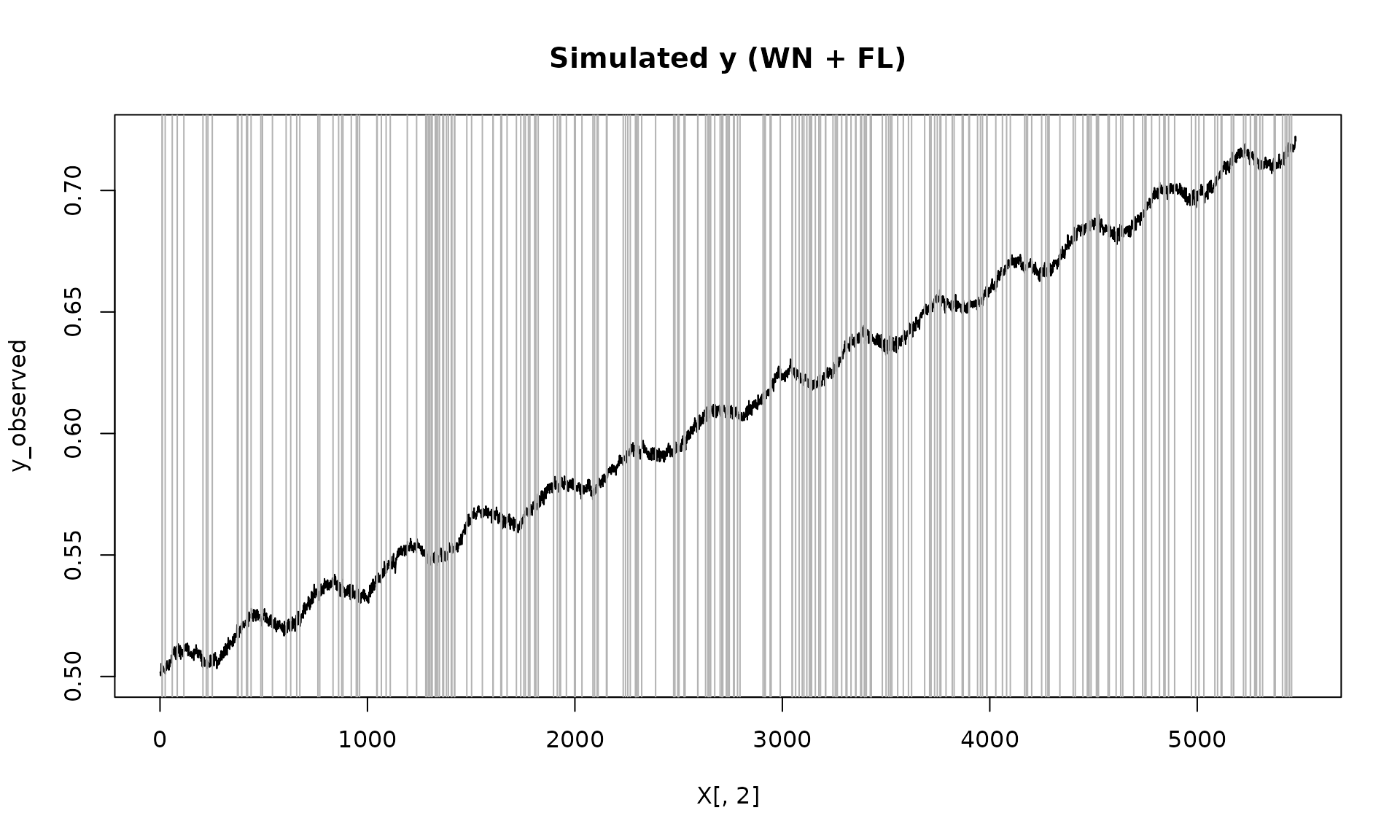
plot(X[, 2], y_observed, type = "l", main = "Simulated y (WN + FL)")
id_not_observed = which(is.na(y_observed))
for(i in id_not_observed){
  abline(v = X[i, 2], col = "grey70", lty =1)
}

Fit model

fit_fl = gmwmx2(X = X, y = y_observed, model = wn() + flicker())
fit_fl

## GMWMX fit
##        Estimate Std.Error
## beta1 4.996e-01 9.208e-04
## beta2 4.022e-05 2.913e-07
## beta3 4.993e-03 1.496e-04
## beta4 6.913e-04 1.461e-04
## 
## Missingness model
##   Proportion missing : 0.0482 
##   p1                 : 0.0482 
##   p2                 : 0.9508 
##   p*                 : 0.9518 
## 
## Stochastic model
##   Sum of 2 processes
##   [1] White Noise
##        Estimated parameters : sigma2 = 8.366e-07 
##   [2] Flicker
##        Estimated parameters : sigma2 = 9.952e-07 
## 
## Runtime (seconds)
##   Total              : 2.5905

Monte Carlo simulation

B_fl = 100
mat_res_fl = matrix(NA, nrow = B_fl, ncol = 18)
for(b in seq(B_fl)){
  eps = generate(wn(sigma2_wn_fl) + flicker(sigma2 = sigma2_fl),
                 n = n, seed = (123 + b))$series
  y = X %*% beta + eps


  Z = generate(mod_missing, n = n, seed = (123 + b))
  Z_process = Z$series
  y_observed = ifelse(Z_process == 1, y, NA)



  fit = gmwmx2(X = X, y = y_observed, model = wn() + flicker())
  fit2 = lm(y_observed~X[,2] + X[,3] + X[,4])

  mat_res_fl[b, ] = c(fit$beta_hat, fit$std_beta_hat,
                      summary(fit2)$coefficients[,1],
                      summary(fit2)$coefficients[,2],
                      fit$theta_domain$`Flicker_2`,
                      fit$theta_domain$`White Noise_1`)
  # cat("Iteration ", b, " \n")
}

Plot empirical distributions of estimated parameters

mat_res_fl_df = as.data.frame(mat_res_fl)
colnames(mat_res_fl_df) = c("gmwmx_beta0_hat", "gmwmx_beta1_hat",
                            "gmwmx_beta2_hat", "gmwmx_beta3_hat",
                            "gmwmx_std_beta0_hat", "gmwmx_std_beta1_hat",
                            "gmwmx_std_beta2_hat", "gmwmx_std_beta3_hat",
                            "lm_beta0_hat", "lm_beta1_hat", "lm_beta2_hat", "lm_beta3_hat",
                            "lm_std_beta0_hat", "lm_std_beta1_hat",
                            "lm_std_beta2_hat", "lm_std_beta3_hat",
                            "sigma2_fl" ,"sigma2_wn")

par(mfrow = c(1, 4))
boxplot_mean_dot(mat_res_df[, c("gmwmx_beta0_hat")],las=1,
                 names = c("beta0"),
                 main = expression(beta[0]), ylab = "Estimate")
abline(h = beta[1], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta1_hat")],las=1,
                 names = c("beta1"),
                 main = expression(beta[1]), ylab = "Estimate")
abline(h = beta[2], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta2_hat")],las=1,
                 names = c("beta2"),
                 main = expression(beta[2]), ylab = "Estimate")
abline(h = beta[3], col = "black", lwd = 2)

boxplot_mean_dot(mat_res_df[, c("gmwmx_beta3_hat")],las=1,
                 names = c("beta3"),
                 main = expression(beta[3]), ylab = "Estimate")
abline(h = beta[4], col = "black", lwd = 2)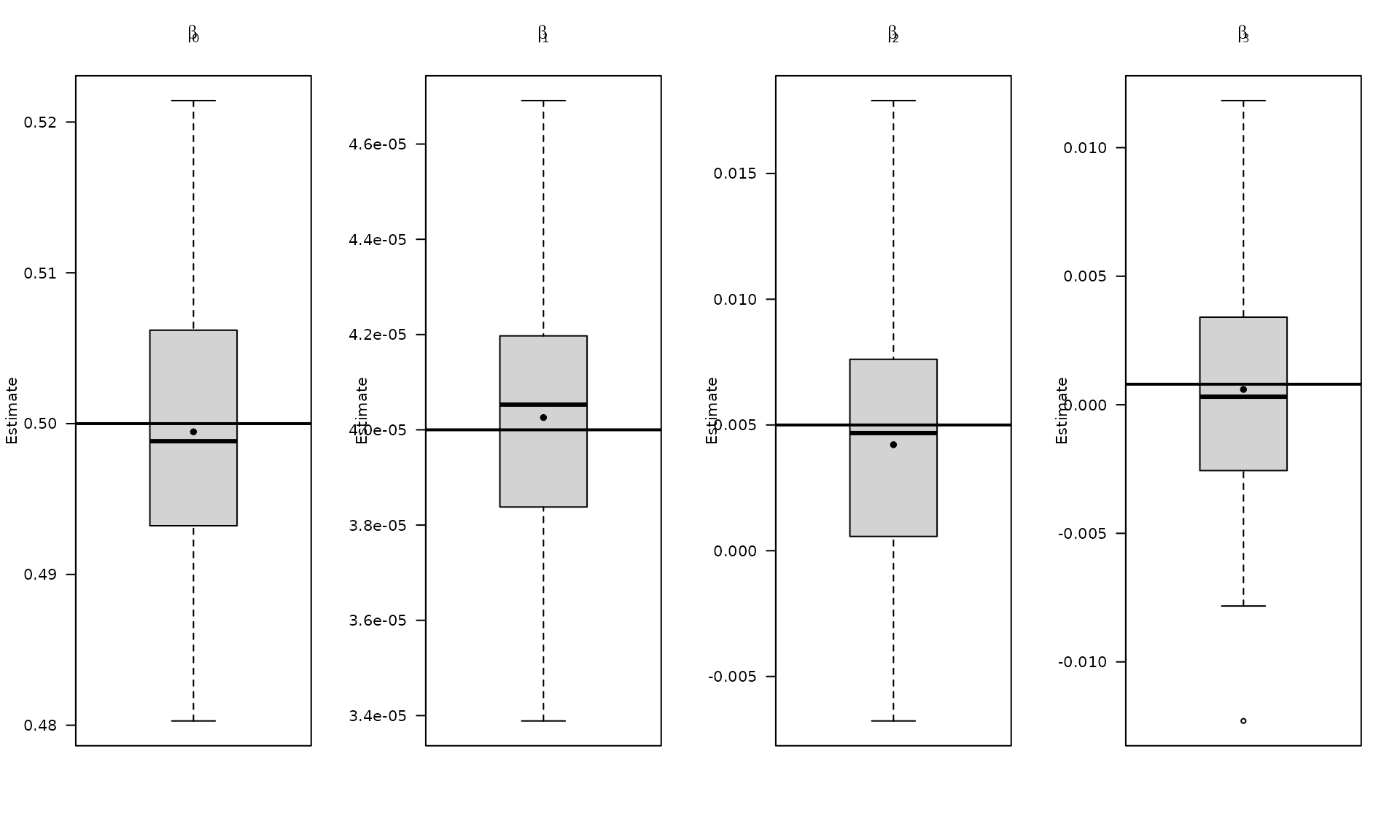

par(mfrow = c(1, 1))

par(mfrow = c(1, 2))

boxplot_mean_dot(mat_res_fl_df$sigma2_fl,las=1,
                 main = expression(sigma["FL"]^2), ylab = "Estimate")
abline(h = sigma2_fl, col = "black", lwd = 2)

boxplot_mean_dot(mat_res_fl_df$sigma2_wn,las=1,
                 names = c("phi_ar1"),
                 main = expression(sigma["WN"]^2), ylab = "Estimate")
abline(h = sigma2_wn_fl, col = "black", lwd = 2)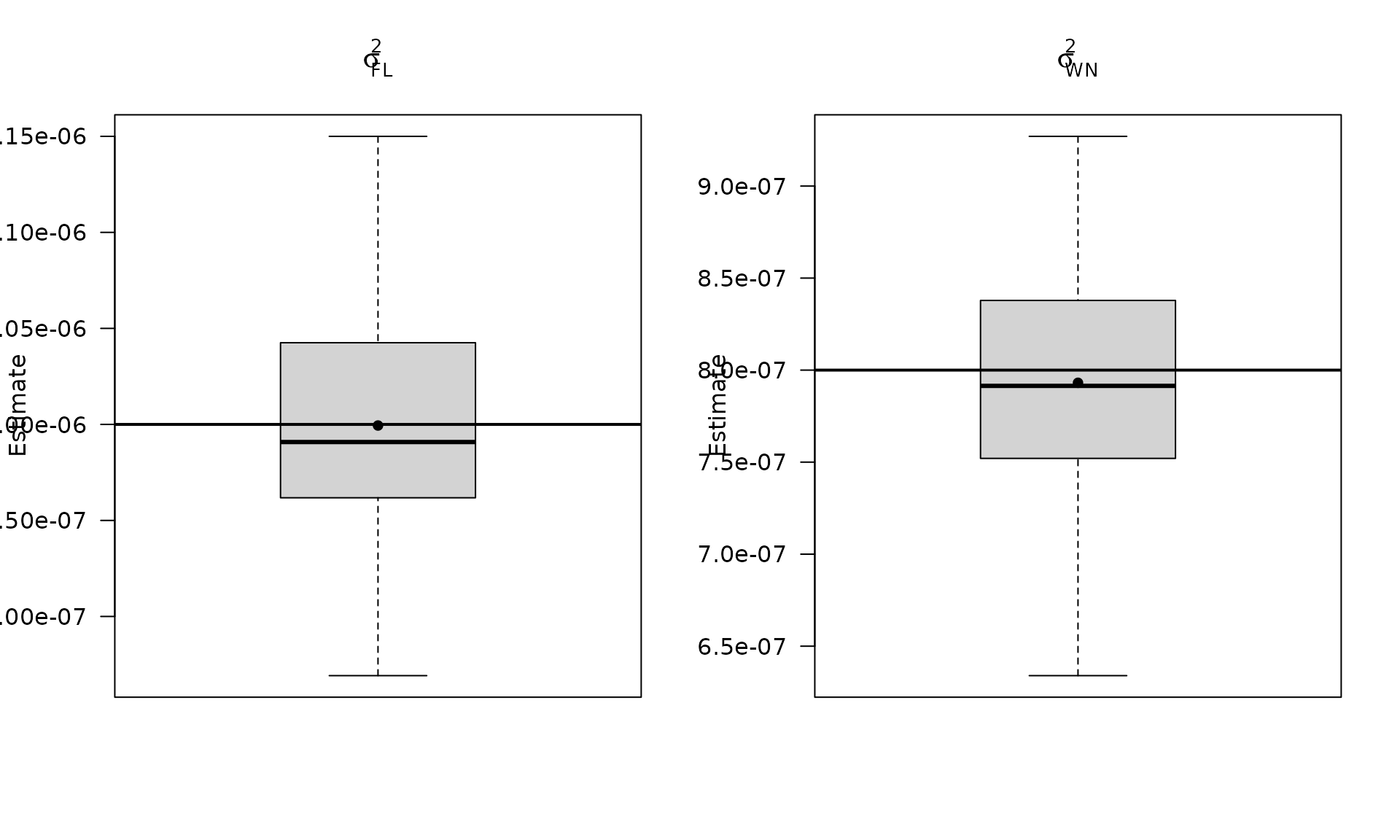

par(mfrow = c(1, 1))

Compute empirical coverage of confidence intervals

# Compute empirical coverage of confidence intervals for beta

zval = qnorm(0.975)
mat_res_fl_df$upper_ci_gmwmx_beta1 = mat_res_fl_df$gmwmx_beta1_hat + zval * mat_res_fl_df$gmwmx_std_beta1_hat
mat_res_fl_df$lower_ci_gmwmx_beta1 = mat_res_fl_df$gmwmx_beta1_hat - zval * mat_res_fl_df$gmwmx_std_beta1_hat
# empirical coverage of gmwmx beta
dplyr::between(rep(beta[2], B_fl), mat_res_fl_df$lower_ci_gmwmx_beta1, mat_res_fl_df$upper_ci_gmwmx_beta1) %>% mean()

## [1] 0.94

# do the same for lm beta
mat_res_fl_df$upper_ci_lm_beta1 = mat_res_fl_df$lm_beta1_hat + zval * mat_res_fl_df$lm_std_beta1_hat
mat_res_fl_df$lower_ci_lm_beta1 = mat_res_fl_df$lm_beta1_hat - zval * mat_res_fl_df$lm_std_beta1_hat
dplyr::between(rep(beta[2], B_fl), mat_res_fl_df$lower_ci_lm_beta1, mat_res_fl_df$upper_ci_lm_beta1) %>% mean()

## [1] 0.07