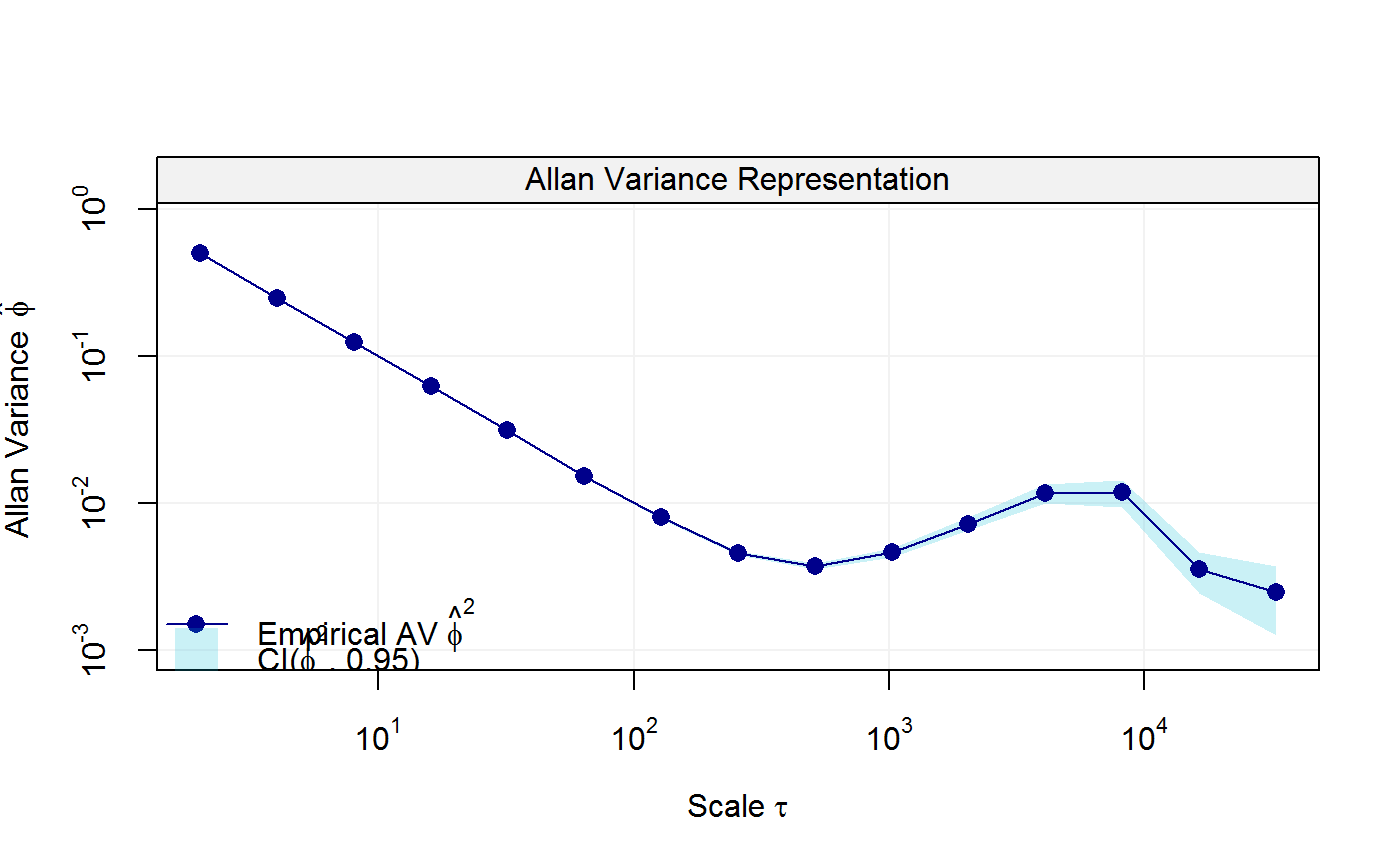
Computes the Allan Variance Linear Regression estimator

Source: R/avlr.R

Estimate the parameters of time series models based on the Allan Variance Linear Regression (AVLR) approach

avlr(x, ...)

# S3 method for default
avlr(x, qn = NULL, wn = NULL, rw = NULL,
  dr = NULL, ci = FALSE, B = 100, alpha = 0.05, ...)

# S3 method for imu_avar
avlr(x, qn_gyro = NULL, wn_gyro = NULL,
  rw_gyro = NULL, dr_gyro = NULL, qn_acc = NULL, wn_acc = NULL,
  rw_acc = NULL, dr_acc = NULL, B = 100, alpha = 0.05, ...)

Arguments

x

A vec of time series observations or an imu object.
...

Further arguments passed to other methods.
qn

A vec specifying on which scales the parameters of a Quantization Noise (QN) should be computed.
wn

A vec specifying on which scales the parameters of a White Noise (WN) should be computed.
rw

A vec specifying on which scales the parameters of a Random Wakk (RW) should be computed.
dr

A vec specifying on which scales the parameters of a Drift (DR) should be computed.
ci

A boolean to compute parameter confidence intervals.
B

A double for the number of bootstrap replicates to compute the parameter confidence intervals.
alpha

A double defining the level of the confidence interval (1 - `alpha`).
qn_gyro

A vec specifying on which scales the parameters of a Quantization Noise (QN) should be computed for the gyroscope component.
wn_gyro

A vec specifying on which scales the parameters of a White Noise (WN) should be computed for the gyroscope component.
rw_gyro

A vec specifying on which scales the parameters of a Random Wakk (RW) should be computed for the gyroscope component.
dr_gyro

A vec specifying on which scales the parameters of a Drift (DR) should be computed for the gyroscope component.
qn_acc

A vec specifying on which scales the parameters of a Quantization Noise (QN) should be computed for the accelerometer component.
wn_acc

A vec specifying on which scales the parameters of a White Noise (WN) should be computed for the accelerometer component.
rw_acc

A vec specifying on which scales the parameters of a Random Wakk (RW) should be computed for the accelerometer component.
dr_acc

A vec specifying on which scales the parameters of a Drift (DR) should be computed for the accelerometer component.

Value

If the input x is a vec, then the function returns a list that contains:

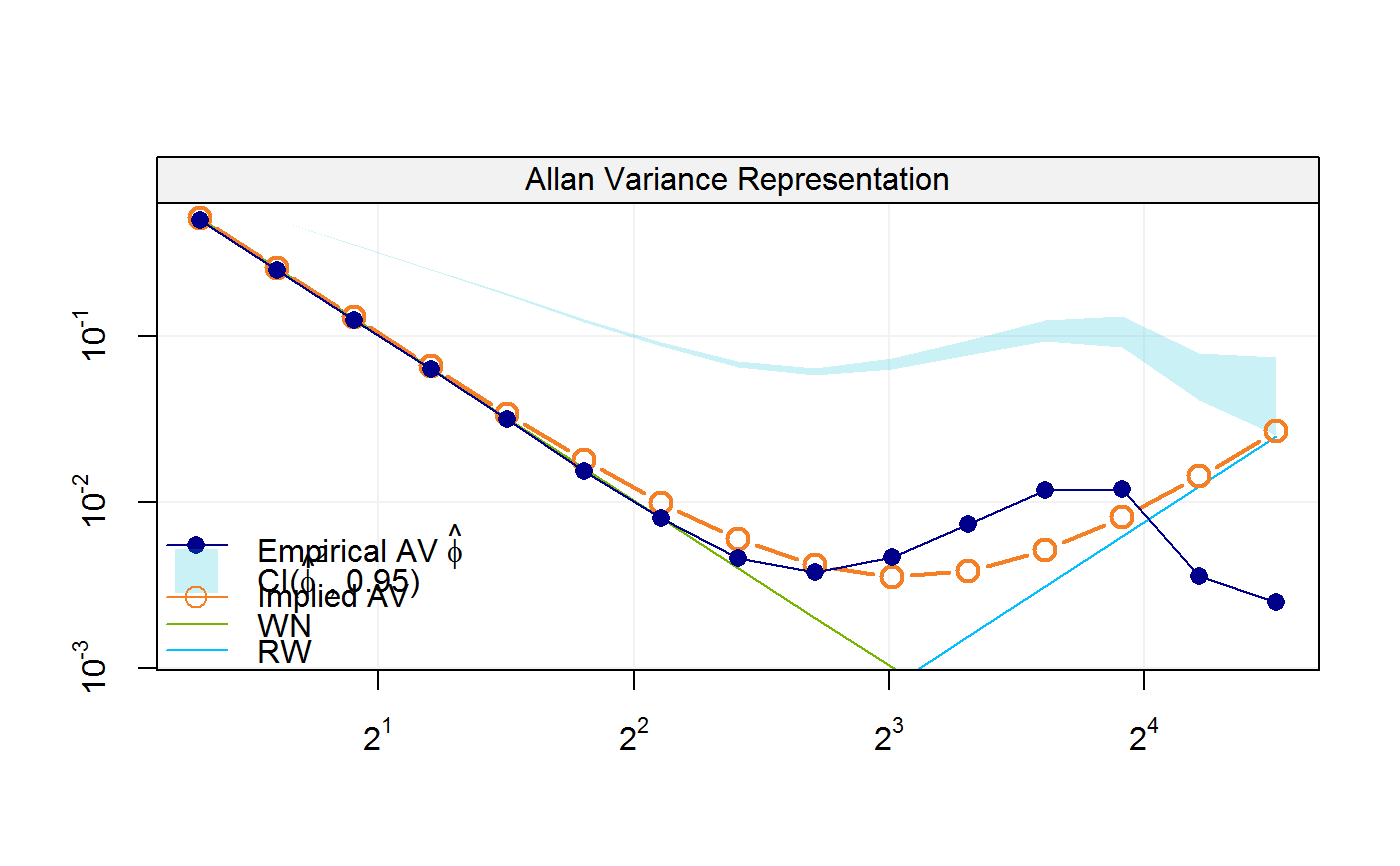
  • "estimates": The estimated value of the parameters.

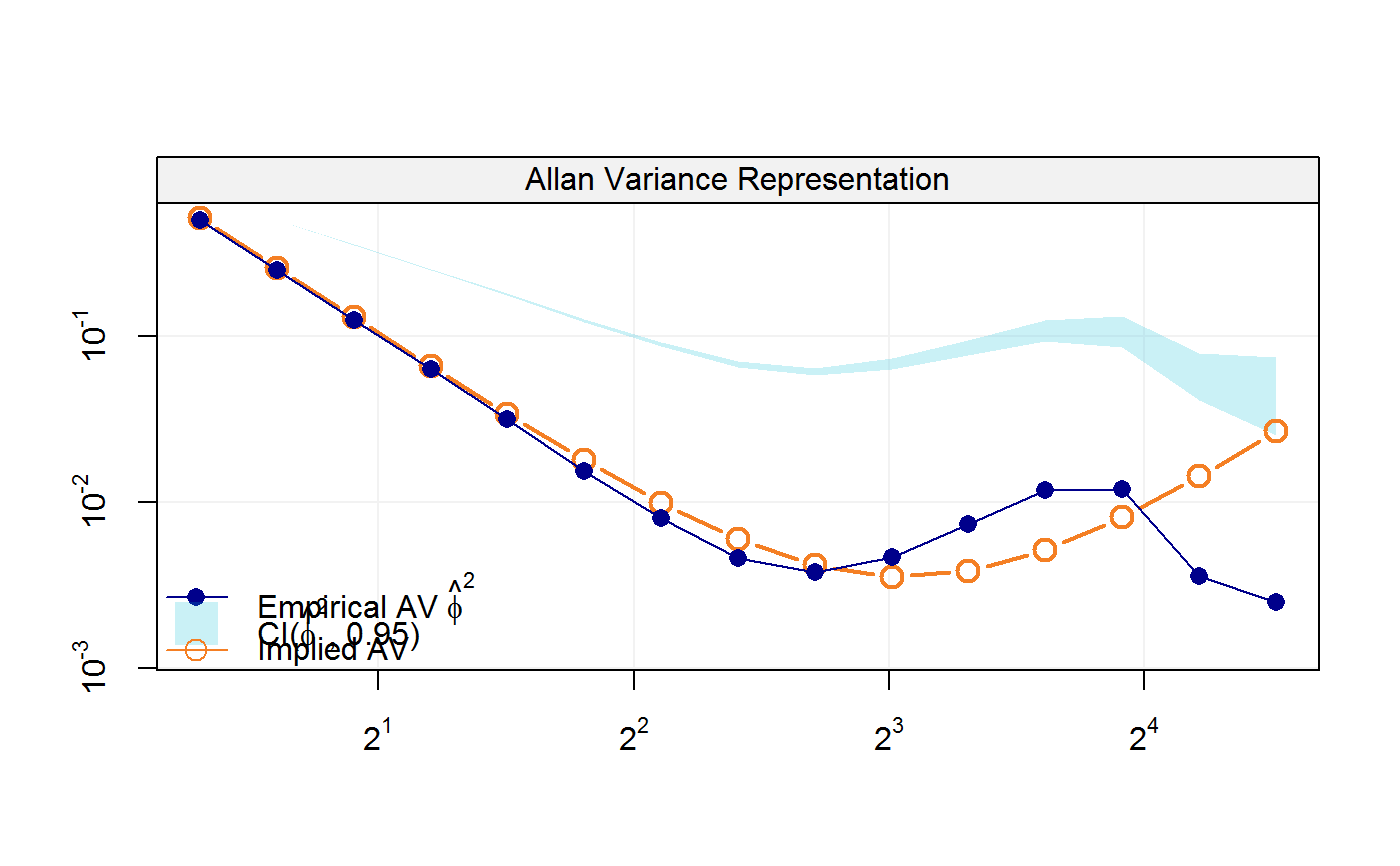
  • "implied_ad": The Allan deviation implied by the estimated parameters.

  • "implied_ad_decomp": The Allan deviation implied by the estimated parameters for each individual model (if more than one is specified).

  • "av": The avar object computed from the provided data.

If the input x is of the class imu_avar, then the function returns a list that contains:

  • "gyro": The estimation results correseponding to the gyroscope component.

  • "acc": The estimation results correseponding to the accelerometer component.

  • "imu_av": The imu_avar object computed based on the IMU data.

Examples

set.seed(999)

N = 100000
Xt = rnorm(N) + cumsum(rnorm(N, 0, 3e-3))

av = avar(Xt)
plot(av)

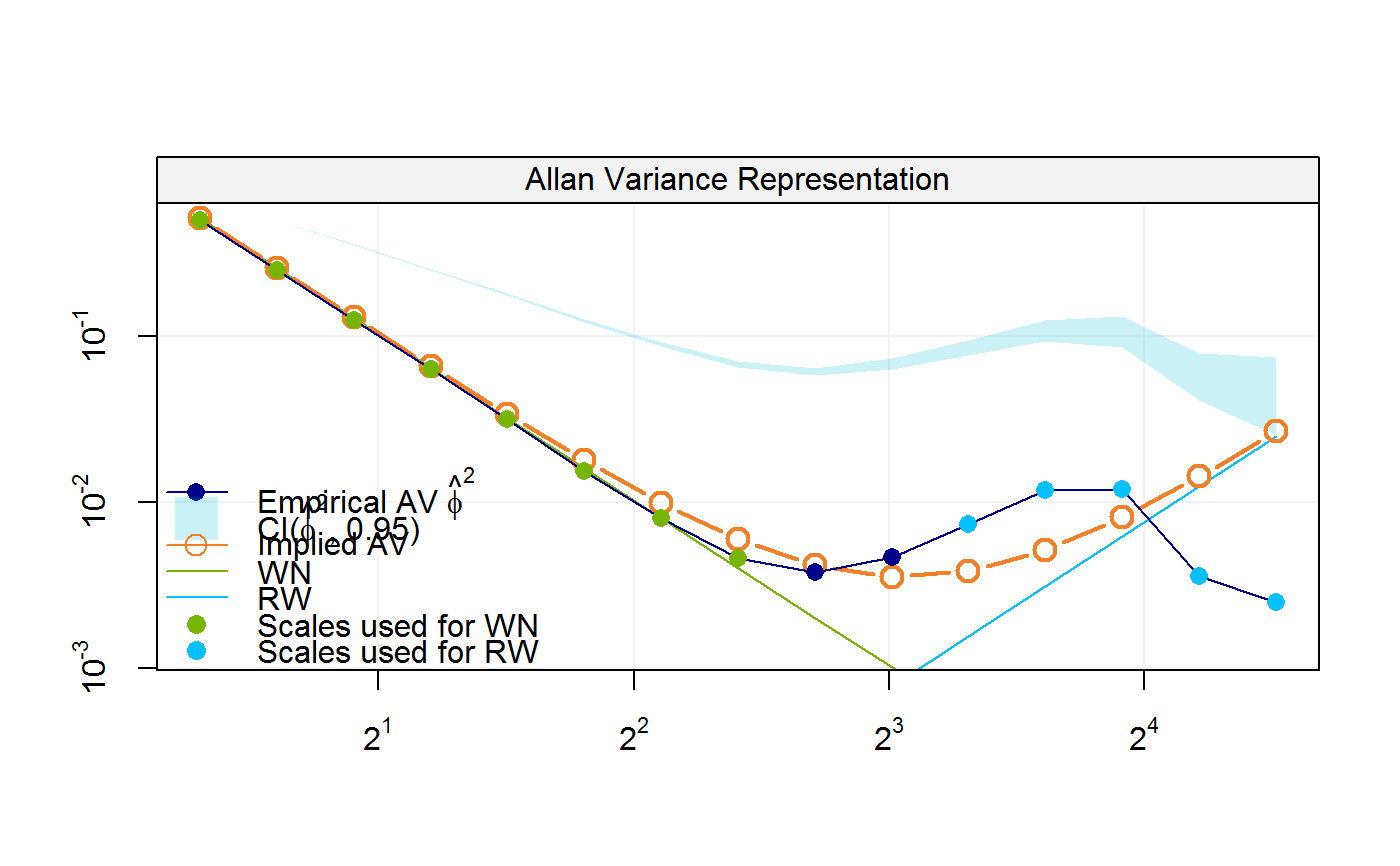
# Input time series
fit = avlr(Xt, wn = 1:8, rw = 11:15)
fit
#> 
#>  Estimates: 
#>          Value
#> WN 1.013398300
#> RW 0.001508291

# Input directly Allan variance
fit = avlr(av, wn = 1:8, rw = 11:15)
fit
#> 
#>  Estimates: 
#>          Value
#> WN 1.013398300
#> RW 0.001508291

# Plot functions
plot(fit)
plot(fit, decomp = TRUE)
plot(fit, decomp = TRUE, show_scales = TRUE)