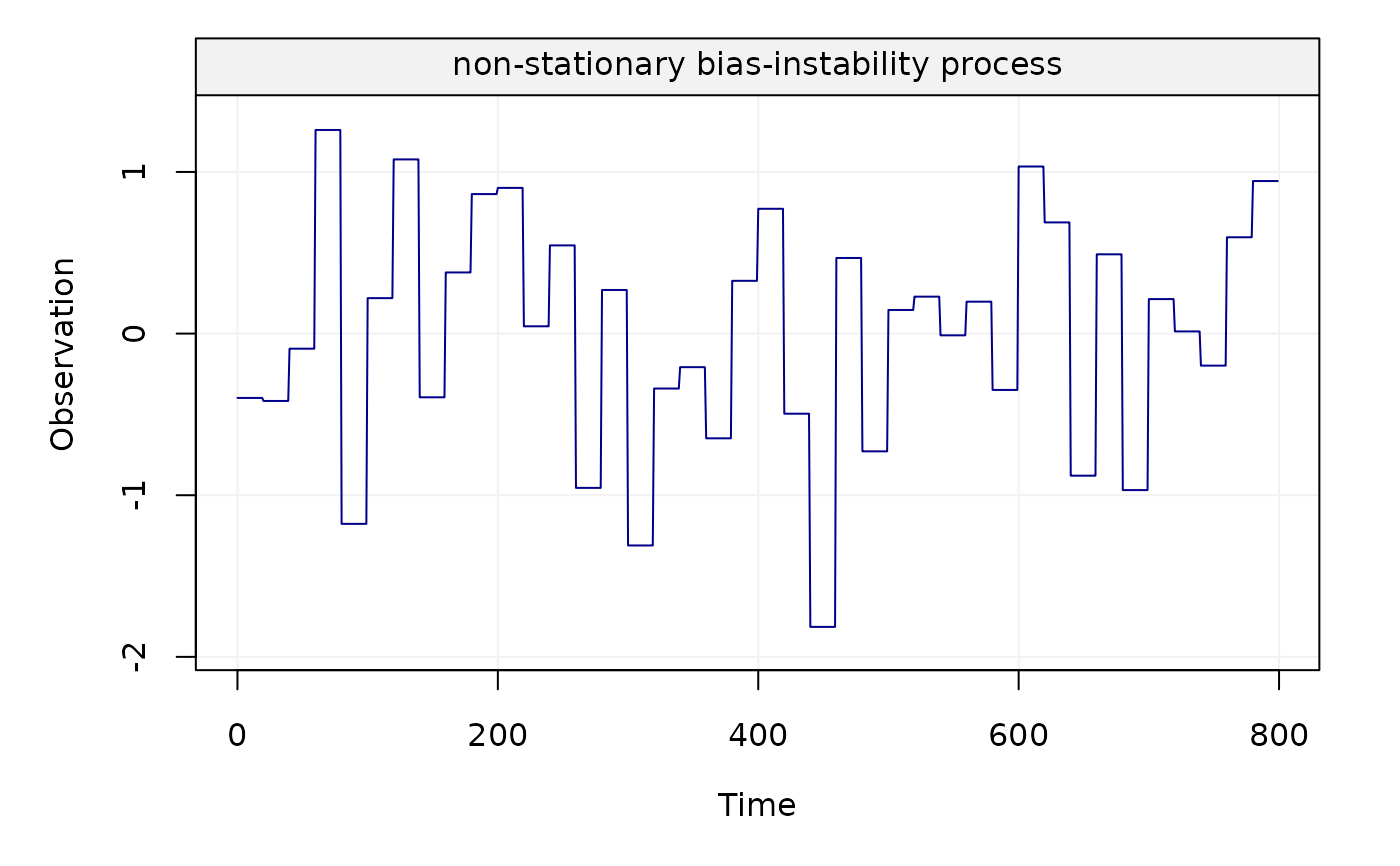
Generate Bias-Instability Process

This function allows to generate a non-stationary bias-instability process.

gen_bi(sigma2, n_total, n_block, title = NULL, seed = 135, ...)

Arguments

sigma2: A double value for the variance parameter \(\sigma ^2\).
n_total: An integer indicating the length of the simulated bias-instability process.
n_block: An integer indicating the length of each block of the bias-instability process.
title: A string defining the name of the time series data.
seed: An integer defined for simulation replication purposes.
...: Additional parameters.

Value

A vector containing the bias-instability process.

Note

This function generates a non-stationary bias-instability process whose theoretical maximum overlapping allan variance (MOAV) is close to the theoretical MOAV of the best approximation of this process through a stationary AR(1) process over some scales. However, this approximation is not good enough when considering the logarithmic representation of the allan variance. Therefore, the exact form of the allan variance of this non-stationary process allows us to better interpret the signals characterized by bias-instability, as shown in "A Study of the Allan Variance for Constant-Mean Non-Stationary Processes" by Xu et al. (IEEE Signal Processing Letters, 2017), preprint available: https://arxiv.org/abs/1702.07795.

Author

Yuming Zhang

Examples

Xt = gen_bi(sigma2 = 1, n_total = 1000, n_block = 10)
plot(Xt)


Yt = gen_bi(sigma2 = 0.8, n_total = 800, n_block = 20,
title = "non-stationary bias-instability process")
plot(Yt)